Hai dây dẫn thẳng , dài song song cách nhau 10 (cm) đặt tại A và B trong không khí vuông góc với mặt phẳng hình vẽ , dòng điện chạy trên dây 1 là I1 = 2 ( A ) , dòng điện chạy trên dây 2 là I2 = 4 (A) , hai dòng điện ngược chiều nhau . Xác định cảm ứng từ tổng hợp do hai dòng điện trên gây ra tại :
a. M là trung điểm AB .
b. N với NA = 6 cm , NB = 8 cm
c. Tính lực từ tác dụng lên mỗi mét chiều dài của mỗi dây ?
...
Đọc tiếp
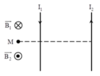
Hai dây dẫn thẳng , dài song song cách nhau 10 (cm) đặt tại A và B trong không khí vuông góc với mặt phẳng hình vẽ , dòng điện chạy trên dây 1 là I1 = 2 ( A ) , dòng điện chạy trên dây 2 là I2 = 4 (A) , hai dòng điện ngược chiều nhau . Xác định cảm ứng từ tổng hợp do hai dòng điện trên gây ra tại :
a. M là trung điểm AB .
b. N với NA = 6 cm , NB = 8 cm
c. Tính lực từ tác dụng lên mỗi mét chiều dài của mỗi dây ?
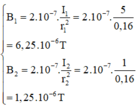
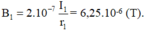
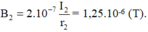
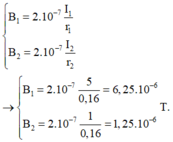
Máy lỗi rồi :(( Bỏ qua phần thừa ở giữa hộ mình nhé
Lắp công thức vô rồi triển thôi bạn :
a/ Lý luận chút: Giả sử dòng điện dây thứ nhất có hướng từ dưới lên=> vecto cảm ứng từ \(\overrightarrow{B_{1M}}\) có kí hiệu là dấu cộng, tương tự với vecto cảm ứng từ \(\overrightarrow{B_{2M}}\) có kí hiệu là dấu chấm (sử dụng quy tắc bàn tay phải)
Vậy 2 lực tác dụng lên M có hướng ngược chiều nhau
\(B_{1M}=2.10^{-7}.\frac{I_1}{r_1}=2.10^{-7}.\frac{2}{0,05}=8.10^{-6}\left(T\right)\)
\(B_{2M}=2.10^{-7}.\frac{I_2}{r_2}=2.10^{-7}.\frac{4}{0,05}=16.10^{-6}\left(T\right)\)
\(\Rightarrow\sum B=\left|B_{1M}-B_{2M}\right|=\left|8.10^{-6}-16.10^{-6}\right|=8.10^{-6}\left(T\right)\)
b/ N cùng 3 điểm A và B tạo thành 1 tam giác vuông
Lắp công thức vô rồi triển thôi bạn :
a/ Lý luận chút: Giả sử dòng điện dây thứ nhất có hướng từ dưới lên=> vecto cảm ứng từ  có kí hiệu là dấu cộng, tương tự với vecto cảm ứng từ  có kí hiệu là dấu chấm (sử dụng quy tắc bàn tay phải)
Vậy 2 lực tác dụng lên M có hướng ngược chiều nhau
b/ N cùng 3 điểm A và B tạo thành 1 tam giác vuông
Gọi hình nhiếu của N lên dây dẫn 1 là H, lên dây dẫn 2 là K
\(\widehat{NAH}=\widehat{NBA};\sin\widehat{NBA}=\sin\widehat{NAH}=\frac{NA}{AB}=\frac{3}{5}\)
\(\Rightarrow HN=\sin\widehat{NAH}.0,06=\frac{3}{5}.0,06=0,036\left(m\right)\)
\(\sin\widehat{KBN}=\sin\widehat{NAB}=\frac{NB}{AB}=\frac{4}{5}\)
\(\Rightarrow KN=\sin\widehat{KBN}.0,08=\frac{4}{5}.0,08=0,064\left(m\right)\)
\(\Rightarrow B_{1N}=2.10^{-7}.\frac{I_1}{HN}=2.10^{-7}.\frac{2}{0,036}=\frac{1}{90000}\left(T\right)\)
\(\Rightarrow B_{2N}=2.10^{-7}.\frac{I_2}{KN}=2.10^{-7}.\frac{4}{0,064}=\frac{1}{80000}\left(T\right)\)
\(\Rightarrow\sum B=\left|B_{1N}-B_{2N}\right|=\left|\frac{1}{90000}-\frac{1}{80000}\right|=\frac{1}{720000}\left(T\right)\)
c/ \(F_t=2.10^{-7}.\frac{I_1I_2}{r}.l=2.10^{-7}.\frac{2.4}{0,1}.1=16.10^{-6}\left(N\right)\)