Thẩy một con xúc xắc (cân đối và đồng chất) 10 lần. Tính xác suất có nhiều nhất 2 lần ra mặt không quá 4 chấm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề: Xuất hiện mặt 2 chấm
n(A)=1
n(omega)=6
=>P(A)=1/6

\(\Omega=\left\{\left(i\right)|i=1,2,3,4,5,6\right\}\)
\(\Rightarrow n\left(\Omega\right)=6\)
Gọi \(A:``\) Xuất hiện trên hai mặt chấm\("\)
\(A=\left\{3,4,5,6\right\}\)
\(\Rightarrow n\left(A\right)=4\)
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{4}{6}=\dfrac{2}{3}\)
Không gian mẫu: Ω= {1;2;3;4;5;6} →n(Ω)=6
Gọi biến cố A:" Xuất hiện trên hai mặt chấm"
A ={3;4;5;6} ➝n(A)= 4
Do đó, p(A)=\(\dfrac{n\left(A\right)}{n\left(\Omega\right)}\)=\(\dfrac{4}{6}\)=\(\dfrac{2}{3}\)

Không gian mẫu: \(6.6=36\)
a.
Lần thứ nhất có 1 khả năng thỏa mãn (3 chấm)
Lần thứ 2 bất kì => có 6 khả năng
\(\Rightarrow1.6=6\) khả năng để lần thứ nhất xuất hiện mặt 3 chấm
Xác suất: \(P=\dfrac{6}{36}=\dfrac{1}{6}\)
b.
Xác suất để cả 2 lần đều ko xuất hiện mặt 2 chấm là: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất để ít nhất 1 lần xuất hiện mặt 2 chấm: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
c.
Các trường hợp có số chấm thuận lợi: (1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(3;1);(3;2);(4;1) có 10 trường hợp
Xác suất: \(P=\dfrac{10}{36}=\dfrac{5}{18}\)
Thầy có thể giải thích hơn về câu a và câu b của bài này được không ạ?

Chọn B
Lời giải.
Số phần tử của không gian mẫu là Ω = 6 . 6 = 36
Gọi A là biến cố "Số chấm trên mặt hai lần gieo có tổng bằng 8".
Gọi số chấm trên mặt khi gieo lần một là x
số chấm trên mặt khi gieo lần hai là y
Theo bài ra, ta có
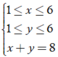
![]()
Khi đó số kết quả thuận lợi của biến cố là Ω A = 5
Vậy xác suất cần tính P ( A ) = 5 36

\(n_{\Omega}=6^3=216\)
a, A: "Tích các số chấm ở mặt xuất hiện trên 3 con xúc sắc chia hết cho 3"
\(\overline{A}\) : "Tích các số chấm ở mặt xuất hiện trên 3 con xúc sắc không chia hết cho 3"
Để xuất hiện TH xảy ra biến cố đối của A thì cả 3 con xúc sắc đều ra số chấm không chia hết cho 3, thuộc {1;2;4;5}
=> \(n_{\overline{A}}=4.4.4=64\)
Vậy, XS của biến cố A là:
\(P_{\left(A\right)}=1-P_{\overline{A}}=1-\dfrac{n_{\overline{A}}}{n_{\Omega}}=1-\dfrac{64}{216}=\dfrac{19}{27}\)
b, B: "Tổng các số chấm ở mặt xuất hiện ba con xúc sắc lớn hơn 4"
=> \(\overline{B}\) : "Tổng các số chấm ở mặt xuất hiện trên ba con xúc sắc không lớn hơn 4"
=> \(\overline{B}=\left\{\left(1;1;1\right);\left(2;1;1;\right);\left(1;2;1\right);\left(1;1;2\right)\right\}\Rightarrow n_{\overline{B}}=4\)
Vậy, XS của biến cố B là:
\(P_{\left(B\right)}=1-P_{\overline{B}}=1-\dfrac{n_{\left(B\right)}}{n_{\Omega}}=1-\dfrac{4}{216}=\dfrac{53}{54}\)
Em không hoán vị cho 2 TH còn lại vì khả năng 2 chấm có thể xuất hiện ở từng viên 1 hả?

omega={1;2;3;4;5;6}
=>n(omega)=6
A={1;2;3;4}
=>n(A)=4
=>P(A)=4/6=2/3
Không gian mẫu: có 6 khả năng xảy ra
Có 4 biến cố thuận lợi là số chấm bằng 1,2,3,4
Do đó xác suất là: \(P=\dfrac{4}{6}=\dfrac{2}{3}\)

Đáp án B
Phương pháp:
Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có nghiệm
⇔ ∆ ≥ 0

![]()
![]()
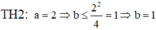
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Gọi A là biến cố:
"Phương trình a x 2 + b x + c = 0 có nghiệm"
![]()
![]()