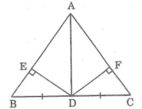
Cho tam giác ABC cân tại A có các đường cao BE và CF. Gọi P là chân đường vuông góc kẻ từ E đến AB, Q là là chân đường vuông góc kẻ từ F đến AC. Chứng minh PQ song song với BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
AB=AC
góc BAE chung
=>ΔAEB=ΔAFC
=>AE=AF
Xét ΔAQF vuong tại Q và ΔAPE vuông tại P có
AF=AE
góc QAF chung
=>ΔAQF=ΔAPE
=>AP=AQ
Xét ΔABC có AP/AB=AQ/AC
nên PQ//BC

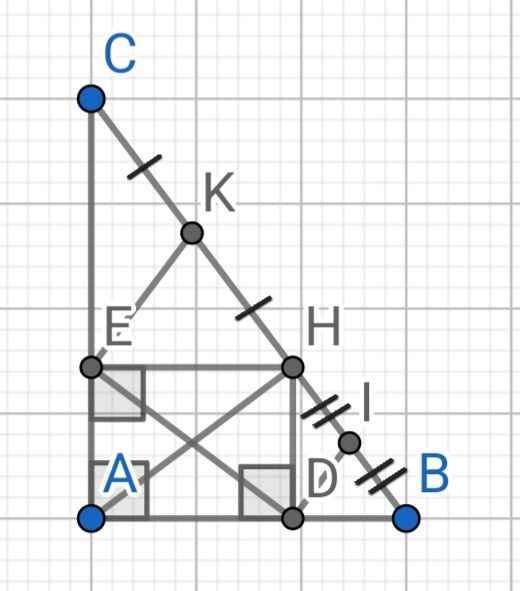 a) Tứ giác ADHE có:
a) Tứ giác ADHE có:
∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)
⇒ ADHE là hình chữ nhật
⇒ AH = DE
b) BHD vuông tại D
I là trung điểm của HB (gt)
⇒ ID = IH = BH : 2
⇒ ∆IDH cân tại I
⇒ ∠IDH = ∠IHD
⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)
= 180⁰ - 2∠IHD (1)
∆CEH vuông tại E
K là trung điểm HC (gt)
⇒ KE = KC = HC : 2
⇒ ∆KEC cân tại K
⇒ ∠KEC = ∠KCE
⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)
= 180⁰ - 2∠KEC (2)
Do HD ⊥ AB (gt)
AC ⊥ AB (gt)
⇒ HD // AC
⇒ ∠IHD = ∠KCE (đồng vị)
⇒ 2∠IHD = 2∠KCE (3)
Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID
Mà ∠CKE và ∠HID là hai góc đồng vị
⇒ DI // KE

1: Xét tứ giác BHEK có \(\widehat{BHE}+\widehat{BKE}=180^0\)
nên BHEK là tứ giác nội tiếp
2: Xét ΔBEA vuông tại E có EH là đường cao
nên \(BH\cdot BA=BE^2\left(1\right)\)
Xét ΔBEC vuông tại E có EK là đường cao
nên \(BK\cdot BC=BE^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)

Vì ΔABC cân tại A và DB = DC (gt) nên đường trung tuyến AD cũng là đường phân giác của ∠(BAC) (tính chất).
Ta có: DE ⊥ AB (gt)
DF ⊥ AC (gt)
Suy ra: DE = DF (tính chất đường phân giác của góc).

Xét tam giác BED và tam giác CFD có:
\(\widehat{BED}=\widehat{CFD}\left(=90^o\right)\)
\(BD=DC\)
\(\widehat{EBD}=\widehat{FCD}\)(tam giác ABC cân)
=>tam giác BED= tam giác CFD (ch-gn)
=> DE=DF

a: Xét tứ giác EAFH có
\(\widehat{EAF}=\widehat{AEH}=\widehat{AFH}=90^0\)
Do đó: EAFH là hình chữ nhật

a: Xét ΔABD và ΔACD có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
c: ΔABC cân tại A
mà AD là phân giác
nen AD vuông góc BC
Xét ΔABC có
AD,BE,CK là các đường cao
=>AD,BE,CK đồng quy