Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ΔABC cân tại A và DB = DC (gt) nên đường trung tuyến AD cũng là đường phân giác của ∠(BAC) (tính chất).
Ta có: DE ⊥ AB (gt)
DF ⊥ AC (gt)
Suy ra: DE = DF (tính chất đường phân giác của góc).

Xét tam giác BED và tam giác CFD có:
\(\widehat{BED}=\widehat{CFD}\left(=90^o\right)\)
\(BD=DC\)
\(\widehat{EBD}=\widehat{FCD}\)(tam giác ABC cân)
=>tam giác BED= tam giác CFD (ch-gn)
=> DE=DF

Vì ΔABC cân tại A và DB DC (gt) nên đường trung tuyến AD cũng là đường phân giác của (BAC).
Ta có: DE ⊥ AB (gt)
DF ⊥ AC (gt)
Suy ra: DE = DF (tính chất đường phân giác của góc)
(ĐPCM)

b) Ta có: BM=CM(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(ΔACB cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
hay AM⊥BC(đpcm)

a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔADB=ΔADC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

a. xét tam giác vuông ADE và tam giác vuông ADF,có :
AB = AC ( ABC cân )
Góc EAD = góc FAD ( gt )
AD : cạnh chung
Vậy tam giác vuông ADE = tam giác vuông ADF ( c.g.c )
=> DE = DF ( 2 cạnh tương ứng )
b. xét tam giác vuông BDE và tam giác vuông CDF, có:
góc B = góc C ( ABC cân )
BD = CD ( AD là đường phân giác cũng là đường trung tuyến trong tam giác cân ABC )
Vậy tam giác vuông BDE = tam giác vuông CDF ( cạnh huyền. góc nhọn)
c. ta có: AD là đường phân giác trong tam giác cân ABC cũng là đường trung trực của BC
a: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
\(\widehat{EAD}=\widehat{FAD}\)
Do đó: ΔAED=ΔAFD
SUy ra: DE=DF
b: Xét ΔBDE vuông tại E và ΔCDF vuông tại F có
BD=CD
DE=DF
Do đó: ΔBDE=ΔCDF
c: Ta có: ΔABC cân tại A
mà AD là phân giác
nên AD là đường trung trực của BC

a,
Ta có : D là trung điểm của BC
Mà Δ ABC cân tại A
=> AD là đường cao
=> AD là đường phân giác \(\widehat{BAC}\)
Xét Δ ABD và Δ ACD, có :
\(\widehat{ADB}=\widehat{ADC}=90^o\)
\(\widehat{ABD}=\widehat{ACD}\) (Δ ABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\) (AD là đường phân giác \(\widehat{BAC}\))
=> Δ ABD = Δ ACD (g.g.g)
b, Ta có : AD là đường cao (cmt)
=> AD ⊥ BC
c, Xét Δ AED và Δ AFD, có :
AD là cạnh chung
\(\widehat{AED}=\widehat{AFD}=90^o\)
\(\widehat{EAD}=\widehat{FAD}\) (AD là đường phân giác \(\widehat{BAC}\))
=> Δ AED = Δ AFD (g.c.g)
=> ED = FD
Xét Δ EBD vuông tại E và Δ FCD vuông tại F, có :
ED = FD
DB = DC (D là trung điểm BC)
=> Δ EBD = Δ FCD (ch - cgv)
d, Ta có : BC = 2DC (D là trung điểm BC)
=>12 = 2DC
=> DC = 6 (cm)
Xét Δ ADC vuông tại D, có :
\(AC^2=AD^2+DC^2\) (định lí Py - ta - go)
=> \(10^2=AD^2+6^2\)
=> \(64=AD^2\)
=> AD = 8 (cm)

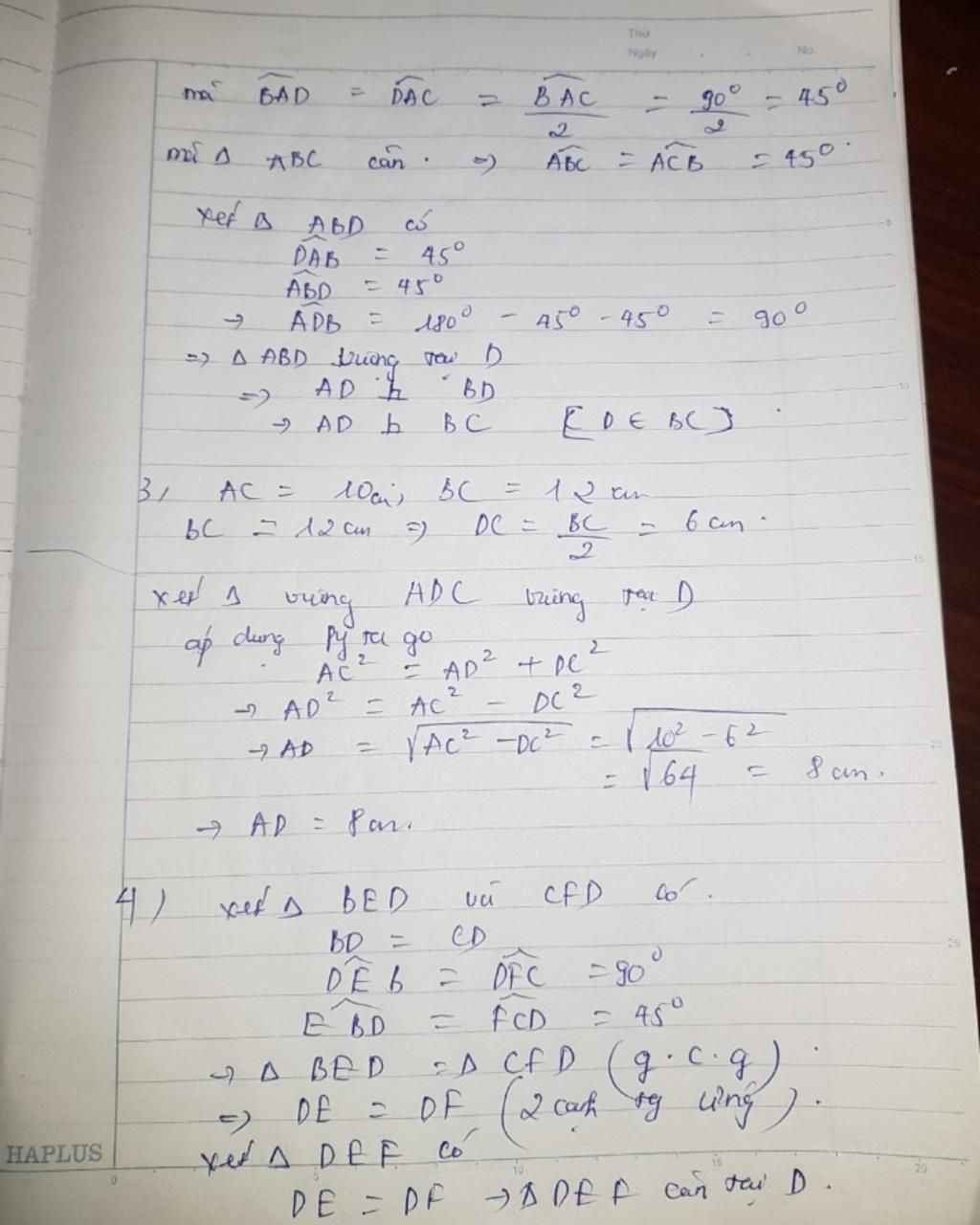
\(\Delta ABC\) cân tại A nên đường trung tuyến AD cũng là đường phân giác.
Theo tính chất tia phân giác của một góc, D thuộc tia phân giác của góc A nên cách đều hai cạnh của góc, do đó DE = DF.