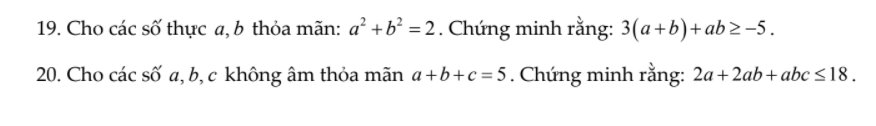Giải giúp mik 2 câu này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình đường tròn (C):
\(\left(x-1\right)^2+\left(y-2\right)^2=3^2\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2=9\)

Đường tròn (C) viết lại: \(\left(x-0\right)^2+\left(y-0\right)^2=3^2\)
Do đó đường tròn có tâm \(I\left(0;0\right)\) và bán kính \(R=3\)

\(\left(x-1\right)^2+\left(y+2\right)^2=25\)
\(\Leftrightarrow x^2-2x+1+y^2+4y+4=25\)
\(\Leftrightarrow x^2+y^2-2x+4y-20=0\)

Đường thẳng d có 1 vtpt là \(\left(1;-2\right)\)
Đường thẳng \(d'\) vuông góc d nên có 1 vtpt là (2;1) (đảo thứ tự tọa độ vtpt của d và đảo dấu 1 trong 2 vị trí tùy thích)
Phương trình d':
\(2\left(x+1\right)+1\left(y-1\right)=0\Leftrightarrow2x+y+1=0\)



1: Xét (O) có
ΔABD nội tiếp
AB là đường kính
Do đó: ΔABD vuông tại D
=>AD\(\perp\)BD tại D
=>BD\(\perp\)AC tại D
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE\(\perp\)EB tại E
=>AE\(\perp\)CB tại E
Xét ΔCAB có
AE,BD là các đường cao
AE cắt BD tại H
Do đó: H là trực tâm của ΔCAB
=>CH\(\perp\)AB tại K
2: ΔCDH vuông tại D
mà DF là đường trung tuyến
nên DF=FH
=>ΔFDH cân tại F
=>\(\widehat{FDH}=\widehat{FHD}\)
mà \(\widehat{FHD}=\widehat{KHB}\)(hai góc đối đỉnh)
và \(\widehat{KHB}=\widehat{DAB}\left(=90^0-\widehat{DBA}\right)\)
nên \(\widehat{FDH}=\widehat{DAB}\)
Ta có: ΔOBD cân tại O
=>\(\widehat{ODB}=\widehat{OBD}=\widehat{DBA}\)
\(\widehat{FDO}=\widehat{FDH}+\widehat{ODB}\)
\(=\widehat{DBA}+\widehat{DAB}=90^0\)
=>DF là tiếp tuyến của (O)

19.
\(\left(a+b\right)^2\le2\left(a^2+b^2\right)=4\Rightarrow-2\le a+b\le2\)
\(P=3\left(a+b\right)+ab=3\left(a+b\right)+\dfrac{\left(a+b\right)^2-\left(a^2+b^2\right)}{2}=\dfrac{1}{2}\left(a+b\right)^2+3\left(a+b\right)-1\)
Đặt \(a+b=x\Rightarrow-2\le x\le2\)
\(P=\dfrac{1}{2}x^2+3x-1=\dfrac{1}{2}\left(x+2\right)\left(x+4\right)-5\ge-5\) (đpcm)
Dấu "=" xảy ra khi \(x=-2\) hay \(a=b=-1\)
20.
Đặt \(P=2a+2ab+abc\)
\(P=2a+ab\left(2+c\right)\le2a+\dfrac{a}{4}\left(b+2+c\right)^2=2a+\dfrac{a}{4}\left(7-a\right)^2\)
\(P\le\dfrac{1}{4}\left(a^3-14a^2+57a-72\right)+18=18-\dfrac{1}{4}\left(8-a\right)\left(a-3\right)^2\le18\) (đpcm)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(3;2;0\right)\)
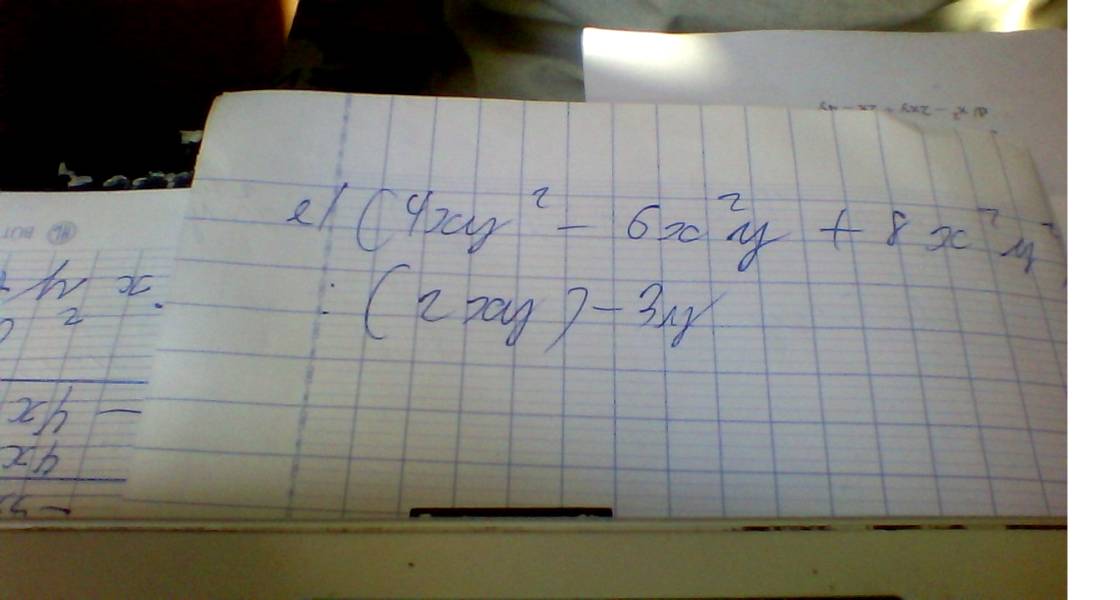





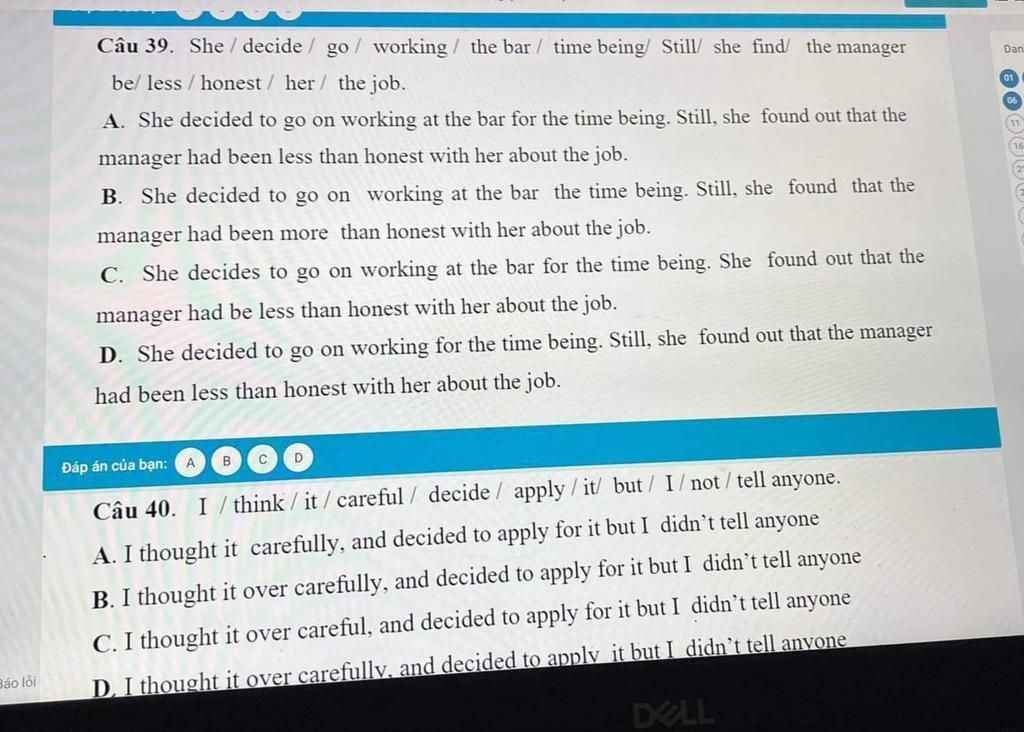
 Giải giúp mik câu này ạ ngày may mik thi r 🥺
Giải giúp mik câu này ạ ngày may mik thi r 🥺