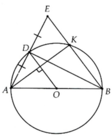
Cho (O) đường kính AB, D là một diểm thuộc đường tròn. E là một điểm đồi xứng A qua D
a) Gọi K là giao điểm Eb với (O). CMR OD _|_ AK
b) Tìm vị trí điểm D trên đường tròn để diện tích ABE lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2019
a, Có O là trung điểm của AB(1)
D là trung điểm của AE ( E đối xứng với A qua D)(2)
Từ (1) và (2)
=> OD là đường trung bình ( t/c đường trung bình )
=>\(\hept{\begin{cases}OD//BE\\OD=\frac{1}{2}BE\end{cases}}\)(t/c đường trung bình )
=>BE=2OD
=>BE=2R (OD=R)
Có AB=BE(=R)
=> \(\Delta ABE\)là \(\Delta\) cân ( đ/n \(\Delta\) cân)
b,Có \(\widehat{AKB}\)là góc nội tiếp chắn nửa đường tròn đường kính AB
=> \(\widehat{AKB}\) =90o (hệ quả góc nội tiếp )
=>AK\(\perp\)KB ( t/c 2 đt vuông góc )
=> AK\(\perp\)BE (K \(\in\)BE)(3)
Mà OD//BE (cmt)(4)
Từ (3) và (4)
=> OD\(\perp\)AK(từ \(\perp\)=> //)
CM
10 tháng 1 2017
a, Chứng minh được ∆BAE cân tại B
b, Chứng minh được DO//BE (tính chất đường trung bình)
c, Mà AK ⊥ BE ( A K B ^ = 90 0 ) => AK ⊥ DO
15 tháng 1 2023
a: Xét (O) có
ΔBDA nội tiép
BA là đường kính
=>ΔBDA vuông tại D
Xét ΔBEA có
BD vừa là đường cao, vừa là trung tuyến
nên ΔBAE cân tại B
b: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
Xét ΔAEBcó AO/AB=AD/AE
nên OD//EB
mà AK vuông góc với EB
nên AK vuông góc với OD
26 tháng 10 2021
a: Xét ΔABE có
O là trung điểm của AB
D là trung điểm của AE
Do đó: OD là đường trung bình của ΔABE
Suy ra: OD//EB
=> AB=AE
hay ΔABE cân tại A
mình làm như vậy đc k