1.Cho tam giác ABC nhọn nội tiếp đường tròn (O). Vẽ đường thẳng vuông góc với
OA sao cho nó cắt các cạnh AB, AC lần lượt tại E và F (E khác A). Chứng minh tam giác
AEF đồng dạng tam giác ACB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 6 2019
Em không vẽ được hình, xin thông cảm
a, Ta có góc EAN= cungEN=cung EC+ cung EN
Mà cung EC= cung EB(E là điểm chính giữa cung BC)
=> góc EAN=cungEB+ cung EN=góc DFE (tính chất góc ở giữa)
=> tam giác AEN đồng dạng tam giác FED
Vậy tam giác AEN đồng dạng tam giác FED
b,Ta có EC=EB=EM
Tam giác EMC cân tại E => EMC=ECM
MÀ EMC+AME=180, ECM+ABE=180
=> AME = ABE
=> tam giác ABE= tam giác AME
=> AB=AM => tam giác ABM cân tại A
Mà AE là phân giác => AE vuông góc BM
CMTT => AC vuông góc EN
MÀ AC giao BM tại M
=> M là trực tâm tam giác AEN
Vậy M là trực tâm tam giác AEN
c, Gọi H là giao điểm OE với đường tròn (O) (H khác E) => O là trung điểm của EH
Vì M là trực tâm của tam giác AEN
=> \(EN\perp AN\)
Mà \(OI\perp AN\)(vì I là trung điểm của AC)
=> \(EN//OI\)
MÀ O là trung điểm của EH
=> I là trung điểm của MH (đường trung bình trong tam giác )
=> tứ giác AMNH là hình bình hành
=> AH=MN
Mà MN=NC
=> AH=NC
=> cung AH= cung NC
=> cung AH + cung KC= cung KN
Mà cung AH+ cung KC = góc KMC(tính chất góc ở giữa 2 cung )
NBK là góc nội tiếp chắn cung KN
=> gócKMC=gócKBN
Hay gócKMC=gócKBM
=> CM là tiếp tuyến của đường tròn ngoại tiếp tam giác MBK( ĐPCM)
Vậy CM là tiếp tuyến của đường tròn ngoại tiếp tam giác BMK
21 tháng 2 2023
xét tam giác MDC và tam giác MBA có
góc M chung
góc MCD = góc MAB (chắn BD)
=> đồng dạng => MD.MA= MB.MC
xét tứ giác AEHF có
góc E+F =180 mà 2 góc ở vị trí đối => nội tiếp
=> góc FEA = góc HAF chắn HF
mà AHF = BCF ( 2 góc phụ nhau )
=> góc BCF = góc AEF
=> tứ giác BEFC nội tiếp
=> ME.MF= MB.MC
=> ME.MF = MD.MA
=> tứ giác AEFD nội tiếp
mà tứ giác AEHF nội tiếp
= > 5 điểm A,E,F,H,D cùng thuộc 1 đường tròn
=> góc ADH = 90
xét (o) có ADK = 90
=> D,H,K thẳng hàng (đpcm )
GN
27 tháng 5 2018
B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)
CM
9 tháng 9 2018
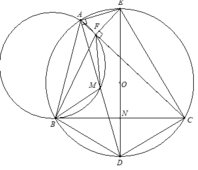
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).
15 tháng 4 2021
Mình đã làm được câu 1,2,3 rồi.Nhờ mọi người giúp câu 4 nha.
AT
21 tháng 6 2021
a) Ta có: \(\angle MEC=\angle MFC=90\Rightarrow MEFC\) nội tiếp
Ta có: \(\angle BDM+\angle BEM=90+90=180\Rightarrow BDME\) nội tiếp
\(\Rightarrow\angle DBM=\angle DEM\)
b) BDME nội tiếp \(\Rightarrow\angle BED=\angle BMD=90-\angle DBM\)
MEFC nội tiếp \(\Rightarrow\angle FEC=\angle FMC=90-\angle ACM\)
mà \(\angle DBM=\angle ACM\) (ABMC nội tiếp)
\(\Rightarrow\angle BED=\angle FEC\) mà B,E,C thẳng hàng \(\Rightarrow D,E,F\) thẳng hàng
Xét \(\Delta MBD\) và \(\Delta MCF:\) Ta có: \(\left\{{}\begin{matrix}\angle MFC=\angle MDB\\\angle MCA=\angle MBD\end{matrix}\right.\)
\(\Rightarrow\Delta MBD\sim\Delta MCF\left(g-g\right)\Rightarrow\dfrac{MB}{MC}=\dfrac{MD}{MF}\Rightarrow MB.MF=MD.MC\)
c) Kẻ đường cao AH,BI
Ta có: \(\angle ARV=\angle ACB=\angle BVH\left(=90-\angle CBI\right)=\angle AVI\)
\(\Rightarrow\Delta AVR\) cân tại A có \(AC\bot VR\Rightarrow AC\) là trung trực VR
mà F nằm trên AC \(\Rightarrow FV=FR\Rightarrow\Delta FVR\) cân tại F \(\Rightarrow\angle FVR=\angle FRV\)
DF cắt BR tại G
\(\angle GRM=\angle BRM=\angle BCM=\angle ECM=\angle EFM=\angle GFM\)
\(\Rightarrow GRFM\) nội tiếp mà \(MF\parallel GR (\bot AC)\) \(\Rightarrow GRFM\) là hình thang cân
\(\Rightarrow\angle MGR=\angle FRG=\angle FRV=\angle FVR\) \(\Rightarrow VF\parallel GM\)
mà \(MF\parallel GR\) \(\Rightarrow VFMG\) là hình bình hành có GF,VM là các đường chéo nên cắt nhau tại trung điểm mỗi đường
\(\Rightarrow DF\) đi qua trung điểm VM
