ai làm hộ mình với...
Đọc tiếp
ai làm hộ mình với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ai làm hộ mình câu 3 với ạ
MQ
0
24 tháng 12 2021
1: Xét (O) có
DC là tiếp tuyến
DA là tiếp tuyến
Do đó: DC=DA
Xét (O) có
EC là tiếp tuyến
EB là tiếp tuyến
Do đó: EC=EB
Ta có: DC+EC=DE
nên DE=AC+EB
D
8 tháng 4 2023
(x+1)+(x+4)+(x+7)+....+(x+28)=155
=>10x+(1+4+....+28)=155
=>10x+[10(1+28)]/2=155
=>10x+145=155
=>10x=10
=>x=1
8 tháng 4 2023
đầu tiên là ta tìm có bao nhiêu số x , ta lấy (28-1):3+1 = 10 (số) . Vậy là có 10 số x và 10 số cộng với x . Rồi ta sẽ tìm tổng của các số cộng với x , ta có : (28+1)x10:2= 145 . Sau đó ta lấy tổng của x và các số kia trừ đi tổng các số cộng với x , đó là : 155-145=10 . Rồi ta lấy 10 đó chia cho 10 số x để tìm 1 số x , ta có : 10:10=1 . Vậy x=1. (nếu đúng thì tick cho tớ nhé ! ) cái này là tớ tự suy luận mà ra .
18 tháng 2 2021
1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
H
6
14 tháng 8 2021
1 , I am neither rich nor poor
2 , She l.i.k.es neither the city nor the country
3 , Neither I nor She is happy
4 , Neither You and She is ready
5 , Neither my mom nor you are fat
6 , She neither write nor phone
7 , He do neither Maths exercise nor English exercise
8 , Neither Jim and Carol has got a car
9 , Neither the teacher nor we come on time
10 , Neither my father nor my mother loves Vietnamese films
* Nếu sai thì thông cảm ạ :) *
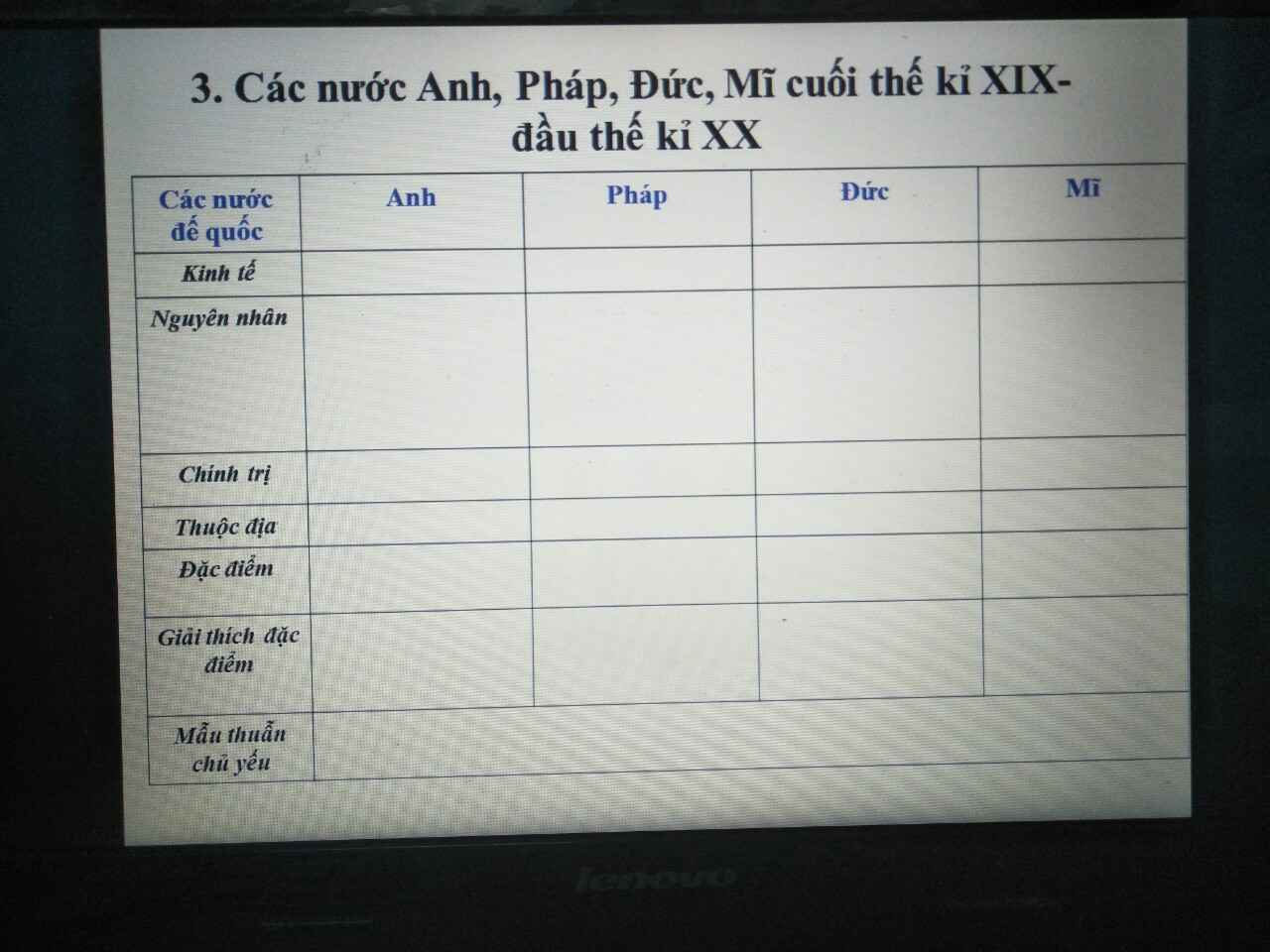Ai làm hộ em với ạ e cần gấp ạ
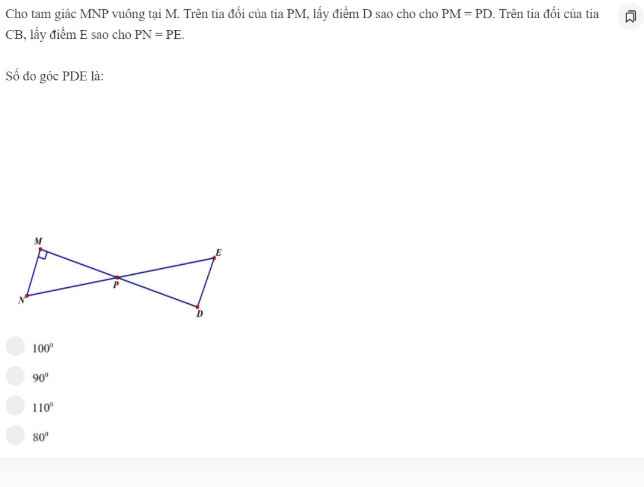ai làm hộ em với ạ !
\(A=-2\left[x^2-2x\left(y+1\right)+\left(y+1\right)^2\right]-8\left(y^2-y+\dfrac{1}{4}\right)+2020\)
\(=-2\left(x-y-1\right)^2-8\left(y-\dfrac{1}{2}\right)^2+2020\le2020\)
\(maxA=2020\Leftrightarrow\)\(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
bạn có thể trả lời chi tiết câu 1 đc không ạ