K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 10 2023
\(tana=\sqrt{3}\)
=>\(\dfrac{sina}{cosa}=\sqrt{3}\)
=>\(sina=\sqrt{3}\cdot cosa\)
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=1+3=4\)
=>\(cos^2a=\dfrac{1}{4}\)
=>\(cosa=\dfrac{1}{2}\)
=>\(sina=\dfrac{\sqrt{3}}{2}\)
\(A=\dfrac{sin^2a-cos^2a}{sina\cdot cosa}\)
\(=\dfrac{\dfrac{3}{4}-\dfrac{1}{4}}{\dfrac{\sqrt{3}}{2}\cdot\dfrac{1}{2}}=\dfrac{2}{4}:\dfrac{\sqrt{3}}{4}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3}\)
HP
24 tháng 9 2021
d. 2x2(x - y) + 2y(y - x)
= 2x2(x - y) - 2y(x - y)
= (2x2 - 2y)(x - y)
= 2(x2 - y)(x - y)
e. 5a2b(a - 2b) - 2a(2b - a)
= 5a2b(a - 2b) + 2a(a - 2b)
= (5a2b + 2a)(a - 2b)
= a(5ab + 2)(a - 2b)
f. 4x2y(x - y) + 9xy2(x - y)
= (4x2y + 9xy2)(x - y)
= xy(4x + 9y)(x - y)
g. 50x2(x - y)2 - 8y2(y - x)2
= 50x2(x2 - 2xy + y2) - 8y2(y2 - 2xy + x2)
= 50x2(x2 - 2xy + y2) - 8y2(x2 - 2xy + y2)
= 50x2(x - y)2 - 8y2(x - y)2
= (50x2 - 8y2)(x - y)2
= 2(25x2 - 4y2)(x - y)2.
LM
0
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
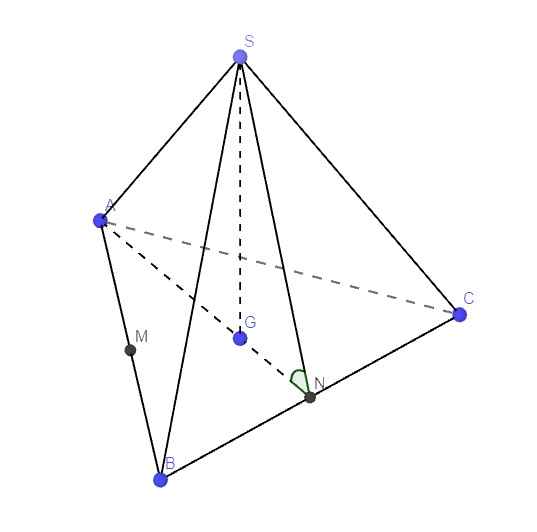
Gọi G là trọng tâm ABC \(\Rightarrow SG\perp\left(ABC\right)\) do S.ABC là chóp đều
\(\Rightarrow SG\perp BC\)
Mà \(AN\perp BC\) (do tam giác ABC đều)
\(\Rightarrow BC\perp\left(SAN\right)\)
\(\Rightarrow\widehat{SNA}\) là góc giữa (ABC) và (SBC)
\(AN=\dfrac{AB.\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(AG=\dfrac{2}{3}AN=\dfrac{2a\sqrt{3}}{3}\) ; \(GN=\dfrac{1}{3}AN=\dfrac{a\sqrt{3}}{3}\) (t/c trọng tâm)
\(SG=\sqrt{SA^2-AG^2}=a\)
\(\Rightarrow tan\widehat{SNA}=\dfrac{SG}{GN}=\sqrt{3}\Rightarrow\widehat{SNA}=60^0\)
10 tháng 4 2023
3:
a: Thay x=2 và y=-2 vào (P), ta được:
4a=-2
=>a=-0,5
b: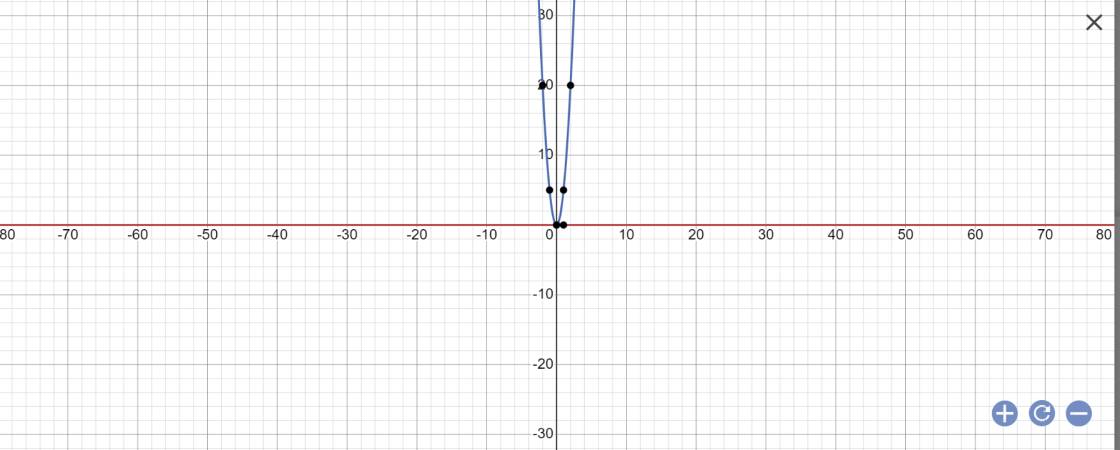 
15 tháng 1 2016
2a)
ta co: A=3^0+3^1+3^2+...........+3^2009
=>2A=3^1+3^2+3^3+...........+3^2010
=>2A=3^2010-3^0=3^2012-1
=>2A<3^2010
19 tháng 7 2023
a,hđt số 3 = \(\left(a^2+2a\right)^2-9\)
b,hđt số 3=\(\left[x-\left(y-6\right)\right]\left[x+\left(y-6\right)\right]\)(đổi dấu làm ngoặc khi trước nó là dấu trừ)=\(x^2-\left(y-6\right)^2\)
19 tháng 7 2023
a) \(\left(a^2+2a+3\right)\left(a^2+2a-3\right)\)
\(=\left(a^2+2a\right)^2+3.\left(-3\right)\)
\(=\left(a^2+2a\right)^2-9\)
b) \(\left(x-y+6\right)\left(x+y-6\right)\)
\(=\left[x-\left(y-6\right)\right]\left[x+\left(y-6\right)\right]\)
\(=x^2-\left(y-6\right)^2\)