
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
\(a,\Leftrightarrow m-1\ne0\Leftrightarrow m\ne1\\ b,\Leftrightarrow m-1>0\Leftrightarrow m>1\\ c,\Leftrightarrow m-1< 0\Leftrightarrow m< 1\)
Bài 2:
\(a,\text{Đồng biến}\Leftrightarrow2m>0\Leftrightarrow m>0\\ \text{Nghịch biến}\Leftrightarrow m-1< 0\Leftrightarrow m< 1\\ b,\Leftrightarrow\left\{{}\begin{matrix}2m=m-1\\m+1\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m\ne2\end{matrix}\right.\Leftrightarrow m=-1\)






\(a^3+b^3+c^3=3abc\)
=>\(\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
=>\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)
=>\(\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
=>\(a^2+b^2+c^2-ab-ac-bc=0\)
=>\(2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)
=>\(\left(a^2-2ba+b^2\right)+\left(b^2-2cb+c^2\right)+\left(a^2-2ac+c^2\right)=0\)
=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
=>\(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow a=b=c\)
\(A=\dfrac{a^{2023}}{b^{2023}}+\dfrac{b^{2023}}{c^{2023}}+\dfrac{c^{2023}}{a^{2023}}\)
\(=\dfrac{a^{2023}}{a^{2023}}+\dfrac{b^{2023}}{b^{2023}}+\dfrac{c^{2023}}{c^{2023}}\)
=1+1+1
=3






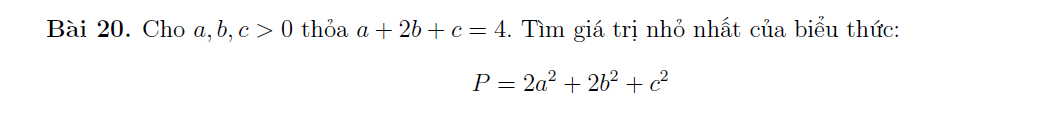


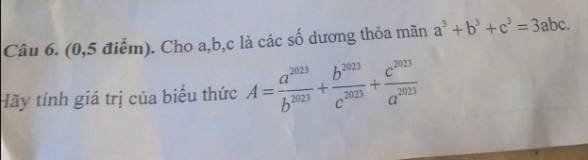
khó nhìn quá bạn