khảo sát sự biến thiên và lập bảng biến thiên
y=\(\dfrac{1}{\sqrt{x}-1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



TXĐ: D=[0;+\(\infty\))
Hàm số này luôn đồng biến với mọi x thuộc D

\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-x_2^2-2x_2+2}{x_1-x_2}\)
\(=\left(x_1+x_2\right)-2\)
Vì \(x_1;x_2\in\left(-\infty;1\right)\) thì \(\left\{{}\begin{matrix}x_1< 1\\x_2< 1\end{matrix}\right.\Leftrightarrow\left(x_1+x_2\right)< 2\)
\(\Leftrightarrow\left(x_1+x_2\right)-2< 0\)
Vậy: Hàm số nghịch biến trên \(\left(-\infty;1\right)\)

\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{-2x_1^2+4x_1+1+2x_2^2-4x_2-1}{x_1-x_2}\)
\(=\dfrac{-2\left(x_1-x_2\right)\left(x_1+x_2\right)+4\left(x_1-x_2\right)}{x_1-x_2}\)
\(=-2\left(x_1+x_2\right)+4\)
Vì \(x_1;x_2\in\left(1;+\infty\right)\) nên \(\left\{{}\begin{matrix}x_1>1\\x_2>1\end{matrix}\right.\Leftrightarrow x_1+x_2>2\)
\(\Leftrightarrow-2\left(x_1+x_2\right)+4< 0\)
Vậy: Hàm số nghịch biến trên \(\left(1;+\infty\right)\)

a: TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-\left(-x\right)^2-2\cdot\left(-x\right)+3\)
\(=-x^2+2x+3\)
\(\Leftrightarrow f\left(-x\right)\ne f\left(x\right)\ne-f\left(x\right)\)
Vậy: Hàm số không chẵn không lẻ
Cái này là xét sự biến thiên: nghịch biến hay đồng biến chứ ạ???

Khảo sát hàm số 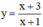
- TXĐ: D = R \ {-1}
- Sự biến thiên:
+ Chiều biến thiên:
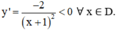
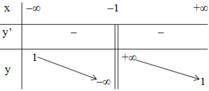
⇒ Hàm số nghịch biến trên các khoảng (-∞; -1) và (-1; +∞).
+ Cực trị: Hàm số không có cực trị.
+ Tiệm cận:
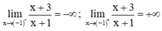
⇒ x = -1 là tiệm cận đứng của đồ thị hàm số.
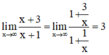
⇒ y = 3 là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
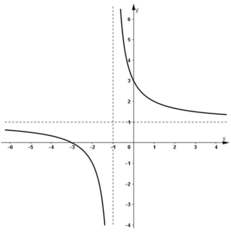
- Đồ thị:
+ Giao với Ox: (-3; 0)
+ Giao với Oy: (0; 3)
+ Đồ thị hàm số nhận (-1; 1) là tâm đối xứng.


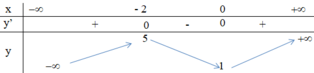
+ Bảng biến thiên:
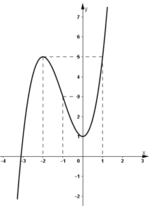
Kết luận:
Hàm số đồng biến trên các khoảng (-∞; -2) và (0; +∞).
Hàm số nghịch biến trên khoảng (-2; 0).
Hàm số đạt cực tiểu tại x = 0 ; y C T = 1 .
Hàm số đạt cực đại tại x = -2 ; y C Đ = 5 .
- Đồ thị:
+ Giao với Oy: (0; 1).
+ Đồ thị (C) đi qua điểm (–3; 1), (1; 5).