Trong không gian tọa độ Oxyz, cho mặt cầu (S): \(x^2+y^2+z^2-2x+4y-2z-8=0\) và mặt phẳng (P): 2x+3y+z-11=0. Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo một đường tròn có bán kính bằng một nửa bán kính mặt cầu (S).
A.\(\left(Q_1\right):2x+3y+z-3+7\sqrt{3}=0;\left(Q_2\right):2x+3y+z-3-7\sqrt{3}=0\)
B. \(\left(Q_1\right):2x+3y+z+3+7\sqrt{3}=0;\left(Q_2\right):2x+3y+z+3-7\sqrt{3}=0\)
C....
Đọc tiếp
Trong không gian tọa độ Oxyz, cho mặt cầu (S): \(x^2+y^2+z^2-2x+4y-2z-8=0\) và mặt phẳng (P): 2x+3y+z-11=0. Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo một đường tròn có bán kính bằng một nửa bán kính mặt cầu (S).
A.\(\left(Q_1\right):2x+3y+z-3+7\sqrt{3}=0;\left(Q_2\right):2x+3y+z-3-7\sqrt{3}=0\)
B. \(\left(Q_1\right):2x+3y+z+3+7\sqrt{3}=0;\left(Q_2\right):2x+3y+z+3-7\sqrt{3}=0\)
C. \(\left(Q_1\right):2x-3y+z+3+7\sqrt{3}=0;\left(Q_2\right):2x-3y+z+3-7\sqrt{3}=0\)
D. \(\left(Q_1\right):2x+3y-z+3+7\sqrt{3}=0;\left(Q_2\right):2x+3y-z+3-7\sqrt{3}=0\)
(Giải thích giùm mình)
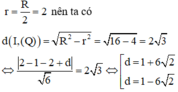
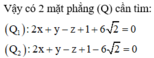
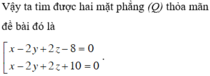
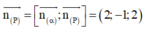
Bán kính mặt cầu: \(R=\sqrt{1^2+\left(-2\right)^2+1^2+8}=\sqrt{14}\)
Tâm mặt cầu: \(I\left(1;-2;1\right)\)
\(\Rightarrow d\left(I;\left(Q\right)\right)=\sqrt{R^2-\left(\frac{R}{2}\right)^2}=\frac{\sqrt{42}}{2}\)
Do (Q) song song (P) nên pt (Q) có dạng: \(2x+3y+z+d=0\)
Áp dụng công thức khoảng cách:
\(d\left(I;\left(Q\right)\right)=\frac{\left|2-6+1+d\right|}{\sqrt{2^2+3^2+1}}=\frac{\sqrt{42}}{2}\)
\(\Leftrightarrow\left|d-3\right|=7\sqrt{3}\Rightarrow\left[{}\begin{matrix}d=3+7\sqrt{3}\\d=3-7\sqrt{3}\end{matrix}\right.\)
Có 2 mặt phẳng thỏa mãn: \(\left[{}\begin{matrix}2x+3y+z+3+7\sqrt{3}=0\\2x+3y+z+3-7\sqrt{3}=0\end{matrix}\right.\)