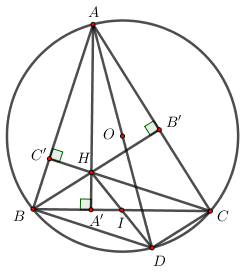
Cho tam giác ABC nhọn, ba đường cao AA’

NT

Nguyễn Thảo Nguyên

19 tháng 4 2020 - olm

Cho tam giác ABC nhọn, ba đường cao AA’; BB’; CC’ cắt nhau tại H. Gọi M là trung điểm của BC. Đương thẳng vuông góc với MH tại H cắt AB và AC theo thứ tự tại I và K.Chứng minh rằng đồng dạng với .Chứng minh rằng đồng dạng với .CHứng minh rằng HI = HK.Chứng minh rằng...

Đọc tiếp

#Toán lớp 8

0

TP

Thủy Phạm Thanh

14 tháng 11 2017 - olm

Cho tam giác ABc nhọn có ba đường cao AA' , BB' , CC" giao nhau ở H. CMR \(\frac{HA}{AA'}-\frac{HB}{BB'}-\frac{HC}{CC'}=1\)

#Toán lớp 9

0

VN

Vũ Nguyễn Phương Thảo

10 tháng 3 2020 - olm

Cho tam giác ABC nhọn có các đường cao AA', BB', CC' và H là trực tâm

Chứng minh BC'.BA+CB'.CA=BC^2

#Toán lớp 8

0

TP

Thủy Phạm Thanh

14 tháng 11 2017 - olm

Cho tam giác ABC nhọn có ba đường cao AA', BB' và CC' cắt nhau ở H. CMR \(\frac{HA}{AA'}+\frac{HB}{BB'}+\frac{HC}{CC'}=1\)

#Toán lớp 9

3

TH

tien hung

7 tháng 4 2019

Ban vao trang Đề thi HSG Toán 8 cấp huyện năm 2016-2017 Phòng GD&ĐT Củ Chi

Đúng(0)

PT

Phạm Thành Đông

9 tháng 3 2021

Đúng(0)

NT

Nguyễn Thị Thúy Ngân

31 tháng 5 2021

Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R), ba đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm đối xứng với H qua BC.a)Chứng minh: Tứ giác ACKB nội tiếp.b)Kẻ đường kính AA' của (O). C/m AA'\(\perp\)EF.c)Gọi I là trung điểm BC. C/m ba điểm H, I, A' thẳng hàng.d)Gọi G là trọng tâm tâm tam giác ABC....

Đọc tiếp

#Toán lớp 9

1

TM

Trần Minh Hoàng

31 tháng 5 2021

a) Dễ thấy A, H, K thẳng hàng.

Ta có \(\widehat{KCB}=\widehat{HCB}=90^o-\widehat{ABC}=\widehat{KAB}\).

Suy ra tứ giác ACKB nội tiếp.

b) \(\widehat{ABD}=\widehat{AA'C};\widehat{ADB}=\widehat{ACA'}=90^o\Rightarrow\Delta ABD\sim\Delta AA'C\left(g.g\right)\Rightarrow\widehat{BAD}=\widehat{A'AC}\)

\(\Rightarrow\widehat{AA'C}=90^o-\widehat{ABC}=90^o-\widehat{AEF}\Rightarrow AA'\perp EF\)

c) Ta có BH // A'C (do cùng vuông góc với AC), CH // A'B (do cùng vuông góc với AB) nên tứ giác BHCA' là hình bình hành. Suy ra H, I, A' thẳng hàng.

d) Do OI là đường trung bình của tam giác A'AH nên OI // AH,\(\dfrac{OI}{AH}=\dfrac{1}{2}=\dfrac{IG}{AG}\Rightarrow\) H, G, O thẳng hàng và \(\dfrac{OG}{HG}=\dfrac{1}{2}\). Từ đó \(S_{AHG}=2S_{AOG}\) (đpcm)

Đúng(0)

TQ

Trần Quân

30 tháng 4 2022

xin hình vẽ

Đúng(0)

NP

Ngọc Phan

24 tháng 3 2016 - olm

Cho tam giác ABC có ba góc nhọn, ba đường cao AA', BB', CC' đồng quy tại H.CMR: \(\frac{HA'}{AA'}+\frac{HB'}{BB'}+\frac{HC'}{CC'}\)bằng một hằng số

#Toán lớp 8

1

NN

Nguyễn Ngọc Anh Minh

CTVHS VIP

24 tháng 3 2016

+ Ta có

\(\frac{S_{HBC}}{S_{ABC}}+\frac{S_{HAC}}{S_{ABC}}+\frac{S_{HAB}}{S_{ABC}}=\frac{S_{HBC}+S_{HAC}+S_{HAB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)

+ Ta có

\(\frac{S_{HBC}}{S_{ABC}}=\frac{\frac{HA'.BC}{2}}{\frac{AA'.BC}{2}}=\frac{HA'}{AA'}\)

+Tương tự ta cũng có

\(\frac{S_{HAC}}{S_{ABC}}=\frac{HB'}{BB'}\) và \(\frac{S_{HAB}}{S_{ABC}}=\frac{HC'}{CC'}\)

=> \(\frac{S_{HBC}}{S_{ABC}}+\frac{S_{HAC}}{S_{ABC}}+\frac{S_{HAB}}{S_{ABC}}=\frac{HA'}{AA'}+\frac{HB'}{BB'}+\frac{HC'}{CC'}=1\) Là một hằng số

Đúng(0)

TQ

Trần Quân

2 tháng 5 2022

Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R), ba đường cao AD, BE, CF cắt nhau tại H. Gọi K là điểm đối xứng với H qua BC.a)Chứng minh: Tứ giác ACKB nội tiếp.b)Kẻ đường kính AA' của (O). C/m AA'⊥⊥EF.c)Gọi I là trung điểm BC. C/m ba điểm H, I, A' thẳng hàng.d)Gọi G là trọng tâm tâm tam giác ABC. C/m SAHG=2SAOGchứng minh ghi rõ...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 6 2023

a: góc HBC+góc HCB=90 độ-góc ACB+90 độ-góc ABC=góc BAC

=>góc BHC+góc BAC=180 độ

H đối xứng K qua BC

=>BH=BK và CH=CK

Xét ΔBHC và ΔBKC có

BH=BK

CH=CK

BC chung

=>ΔBHC=ΔBKC

=>góc BKC=góc BHC

=>góc BKC+góc BAC=180 độ

=>ABKC nội tiếp

b: Gọi Ax là tiếp tuyến của (O) tại A

=>góc xAC=góc ABC=góc AEF

=>EF//Ax

=>EF vuông góc OA

c: Xét tứ giác BHCA' có

BH//CA'

BA'//CH

=>BHCA' là hbh

=>H,I,A' thẳng hàng

Đúng(0)

D

dekhisuki

1 tháng 5 2020 - olm

Cho tam giỏc ABC cú ba góc nhọn, nội tiếp đường tròn tâm O, bán kính R. Kẻ các đường cao AA’, BB’, CC’. Gọi S là diện tớch của tam giỏc ABC và S’ là diện tích của tam giác A’B’C’. 1) Chứng minh rằng AO vuông góc với B’C’

#Toán lớp 9

1

PT

Phạm Thị Mai Anh

10 tháng 5 2020

Giải chi tiết:

a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.

Xét tứ giác AB’HC’ có ∠AB′H+∠AC′H=900+900=1800⇒∠AB′H+∠AC′H=900+900=1800⇒ Tứ giác AB’HC’ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).

b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.

Ta có ∠ABD=900∠ABD=900 (góc nội tiếp chắn nửa đường tròn) ⇒AB⊥BD⇒AB⊥BD.

Mà CH⊥AB(gt)⇒BD∥CHCH⊥AB(gt)⇒BD∥CH

Chứng minh tương tự ta có CD∥BHCD∥BH.

⇒⇒ Tứ giác BHCD là tứ giác nội tiếp (Tứ giác có các cặp cạnh đối song song)

Mà BC∩HD=I(gt)⇒IBC∩HD=I(gt)⇒I là trung điểm của BC.

c) Tính AHAA′+BHBB′+CHCC′AHAA′+BHBB′+CHCC′.

Ta có:

SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′

Chứng minh tương tự ta có: BHBB′=1−SHACSABC;CHCC′=1−SHABSABCBHBB′=1−SHACSABC;CHCC′=1−SHABSABC

⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2

Đúng(0)

LT

Le Thi Khanh Huyen

29 tháng 9 2015 - olm

Cho tam giác ABC có ba góc nhọn. M là một điểm nằm trong tam giác. Gọi A', B', C' theo thứ tự là các hình chiếu của M trên các đường cao AD, BE và CF. Hãy xác định điểm M sao cho AA' = BB' = CC'.

#Toán lớp 7

0

LT

Le Thi Khanh Huyen

28 tháng 9 2015 - olm

Cho tam giác ABC có ba góc nhọn. M là một điểm nằm trong tam giác. Gọi A', B', C' theo thứ tự là các hình chiếu của M trên các đường cao AD, BE và CF. Hãy xác định điểm M sao cho AA' = BB' = CC'.

#Toán lớp 7

0

NK

Nam Khanh Le

10 tháng 4 2018 - olm

Cho tam giác ABC nhọn có các đường cao AA';BB';CC'. Gọi H là trực tâm tam giác ABC. CMR:\( {(AB+BC+AC)^2 \over AA'^2+BB'^2+CC'^2} >=4\)

#Toán lớp 8

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP