Cho hàm số y=f(x) =1/√(2-x). Khẳng định nào sau đây đúng:
A. Hàm số chỉ có giới hạn tại điểm x=2
B. Hàm số có giới hạn trái và giới hạn phải bằng nhau
C. Hàm số có giới hạn tại điểm x=2
D. Hàm số chỉ có giới hạn trái tại điểm x=2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 9 2018
Chọn D
Ta có
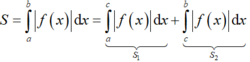
Vì f(x) < 0, ∀ x ∈ a ; c nên |f(x)| = –f(x).
Do đó, S 1 = - ∫ a c f x d x .
Tương tự, f(x) > 0, ∀ x ∈ a ; c nên |f(x)| = f(x).
Do đó, S 2 = ∫ c b f x d x .
Vậy S = - ∫ a c f x d x + ∫ c b f x d x .
thì hàm số là hàm hằng trên K.
thì hàm số nghịch biến trên K.
thì hàm số đồng biến trên K.
CM
18 tháng 6 2018
Đáp án A.
Cho hàm số f(x) có f ' x ≤ 0 ∀ x ∈ ℝ và f '(x) = 0 chỉ tại một số hữu hạn điểm thuộc R. Nên Hàm số f(x) nghịch biến trên R nên ∀ x 1 , x 2 ∈ K ; x 1 < x 2 ⇔ f x 1 > f x 2
Ta có x 1 − x 2 < 0 ; và f x 1 − f x 2 > 0 ⇒ f x 1 − f x 2 x 1 − x 2 < 0
Do \(x< 2\) nên x chỉ tiến tới 2 từ phía trái
Do đó hàm số chỉ có giới hạn trái tại điểm x=2 (giới hạn bằng dương vô cực)