Giúp e vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 6 2023
a: CH=16^2/24=256/24=32/3(cm)
BC=24+32/3=104/3cm
AC=căn 32/3*104/3=16/3*căn 13(cm)
b: BC=12^2/6=144/6=24cm
CH=24-6=18cm
AC=căn 18*24=12*căn 3(cm)
MA
2
23 tháng 12 2021
g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
23 tháng 12 2021
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
TN
1
DT
Đỗ Thanh Hải
CTVVIP
11 tháng 8 2021
1 I wish my students studied hard
2 I wish I could come to the party
3 I wish my grandparents didn't live too far from me
4 Nga wished she were in HN now
5 This room is cleaned everyday
LK
3
18 tháng 2 2023
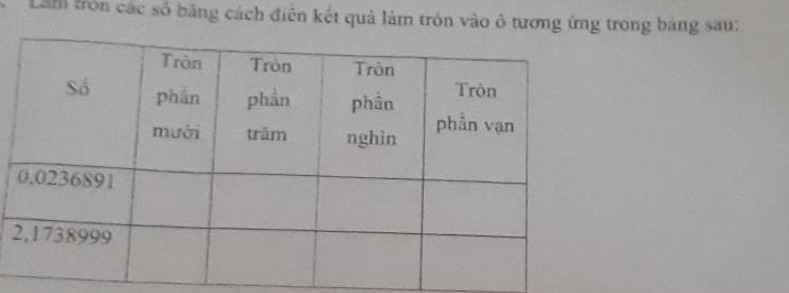
| Số | Phần mười | Phần trăm | Phần nghìn | Phần chục nghìn |
| 0,0236891 | 0,0 | 0,02 | 0,024 | 0,0237 |
| 2,1738999 | 2,2 | 2,17 | 2,174 | 2,1739 |
H9
HT.Phong (9A5)
CTVHS
18 tháng 2 2023
| Số | Tròn phần mười | Tròn phần trăm | Tròn phần nghìn | Tròn phần vạn |
| \(0,0236891\) | \(0,0\) | \(0,02\) | \(0,024\) | \(0,0237\) |
| \(2,1738999\) | \(2,2\) | \(2,17\) | \(2,174\) | \(2,1739\) |
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
TT
4
Q
14 tháng 6 2018
|x+3|+|y-1|=0
\(\Rightarrow\hept{\begin{cases}\left|x+3\right|\ge0\\\left|y-1\right|\ge0\end{cases}\Rightarrow}\hept{\begin{cases}x+3=0\\y-1=0\end{cases}\Rightarrow}\hept{\begin{cases}x=-3\\y=1\end{cases}}\)
Vậy x=-3 ; y=1
DM
1
8 tháng 11 2021
Bài 1:
\(a,\dfrac{25}{14x^2y}=\dfrac{75y^4}{42x^2y^5};\dfrac{14}{21xy^5}=\dfrac{28x}{42x^2y^5}\\ b,\dfrac{3x+1}{12xy^4}=\dfrac{3x\left(3x+1\right)}{36x^2y^4};\dfrac{y-2}{9x^2y^3}=\dfrac{4y\left(y-2\right)}{36x^2y^4}\\ c,\dfrac{1}{6x^3y^2}=\dfrac{6y^2}{36x^3y^4};\dfrac{x+1}{9x^2y^4}=\dfrac{4x\left(x+1\right)}{36x^3y^4};\dfrac{x-1}{4xy^3}=\dfrac{9x^2y\left(x-1\right)}{36x^3y^4}\\ d,\dfrac{3+2x}{10x^4y}=\dfrac{12y^4\left(3+2x\right)}{120x^4y^5};\dfrac{5}{8x^2y^2}=\dfrac{75x^2y^3}{120x^4y^5};\dfrac{2}{3xy^5}=\dfrac{80x^3}{120x^4y^5}\)
