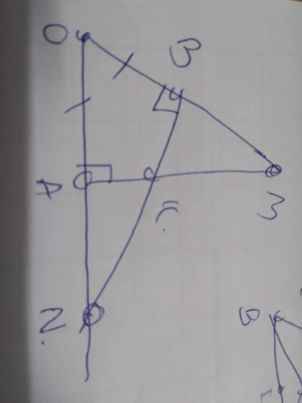
bài 2 : cho góc xOy < 90 độ, kẻ tia phân giác OM, trên tia Ox lấy điểm A, từ điểm A kẻ đường thẳng AM vuông góc OY( M thuộc OY) , AM cắt OM tại D, từ điểm D kẻ thẳng đường vuông góc với Ox đường thẳng đó cắt Ox tại N, cắt Oy tại E.
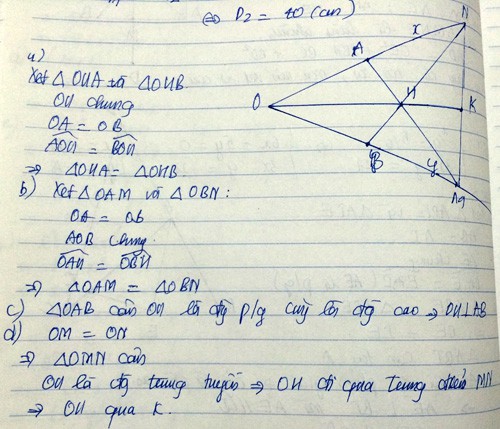
a.chứng minh : tam giác OMD = tam giác OND
b. chứng minh : ME = NA
c. chứng minh : tam giác OAE cân