CHO HÌNH THANG ABCD (AB//CD).GỌI MLAF TRUNG ĐIỂM CD .AM CẮT BD TẠI E BM CẮT AC TẠI F
a)C/M : EF//AB
b) ĐƯỜNG THẲNG EF CẮT AD VÀ BC TẠI H VÀ K . C/M : HE=EF=FK
c) BIẾT AB =7,5 CM , CD=12 CM . TÍNH HK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 4 2023
a: Xét ΔEAB và ΔEMD có
góc EAB=góc EMD
góc AEB=góc MED
=>ΔEAB đồng dạng vơi ΔEMD
=>EM/EA=AB/MD=AB/MC
Xet ΔFAB và ΔFCM có
góc FAB=góc FCM
góc AFB=góc CFM
Do đó: ΔFAB đồng dạng với ΔFCM
=>FB/FM=AB/CM
=>FM/FB=CM/AB=DM/AB=ME/EA
=>EF//AB
b: Xet ΔBMC có FN//MC
nên FN/MC=BN/BC
=>FN/MD=AH/AD
Xét ΔADM có HE//DM
nên HE/DM=AH/AD
Xét ΔBDC có EN//DC
nên EN/DC=BN/BC=AH/AD
=>(EF+FN)/(2DM)=AH/AD=HE/DM=FN/MD
=>(EF+FN)/2=HE=FN
=>EF+FN=2FN
=>FN=EF=HE
31 tháng 1 2022
- Hình vẽ:
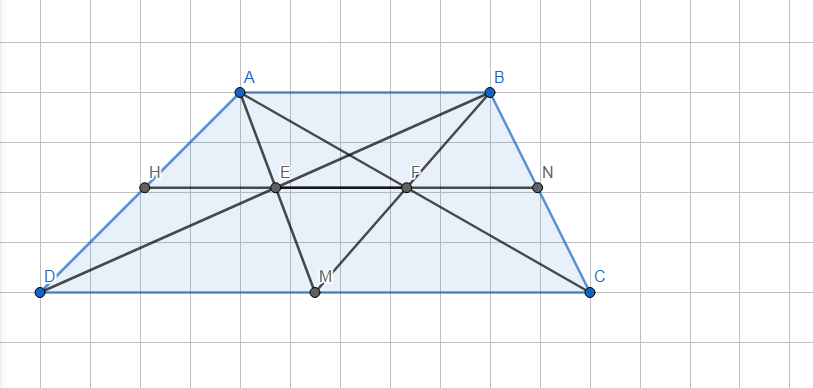
a) - Xét △EDM có:
AB//DM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) (định lí Ta-let) (1).
- Xét △FCM có:
AB//CM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{BF}{MF}=\dfrac{AB}{CM}\) (định lí Ta-let) (2).
- Từ (1) và (2) và \(CM=DM\) (M là trung điểm BC) suy ra:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\).
- Xét △ABM có:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\) (cmt)
=>\(EF\)//\(AB\) (định lí Ta-let đảo)nên\(EF\)//\(AB\)//\(CD\)
b) -Xét △ADM có:
HE//DM (cmt).
=>\(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (định lí Ta-let). (3)
- Xét △ACM có:
EF//CM (cmt)
=>\(\dfrac{EF}{CM}=\dfrac{AE}{AM}\) (định lí Ta-let) (4)
- Từ (3) và (4) và \(DM=CM\) (M là trung điểm BC) suy ra: \(HE=EF\)
-Xét △BDM có:
EF//DM (cmt).
=>\(\dfrac{EF}{DM}=\dfrac{BF}{BM}\)(định lí Ta-let). (5)
- Xét △BCM có:
NF//CM (cmt)
=>\(\dfrac{NF}{CM}=\dfrac{BF}{BM}\) (định lí Ta-let) (6)
- Từ (5) và (6) và \(CM=DM\) (M là trung điểm BC) suy ra: \(NF=EF\)
Mà \(HE=EF\) nên \(HE=EF=NF=\dfrac{1}{3}HN\).
c) -Ta có: \(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (cmt)
=>\(\dfrac{DM}{HE}=\dfrac{AM}{AE}\).
=>\(\dfrac{DM}{HE}-1=\dfrac{EM}{AE}\) (7)
- Ta có: \(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) nên \(\dfrac{EM}{AE}=\dfrac{DM}{AB}\). (8)
- Từ (7) và (8) suy ra:
\(\dfrac{DM}{HE}-1=\dfrac{DM}{AB}\)
=>\(\dfrac{DM}{HE}=\dfrac{DM}{AB}+1=\dfrac{DM+AB}{AB}\)
=>\(HE=\dfrac{AB.DM}{AB+DM}=\dfrac{7,5.\left(12.\dfrac{1}{2}\right)}{7,5+\left(12.\dfrac{1}{2}\right)}=\dfrac{10}{3}\)
=>\(HN=3HE=3.\dfrac{10}{3}=10\) (cm).
18 tháng 8 2016
theo ta-let ta có:
AI trên DK = IB trên KC (=MI trên MK)
AI trên KC = IB trên DK (=IN trên NK)
nhân thẳng hàng dược
AI^ 2 trên DK. KC = IB^2 trên DK .KC
suy ra AI= IB
mà AI trên DK = IB trên KC nên DK= kC
DPCM
Đây : https://hoc24.vn/hoi-dap/tim-kiem?q=Cho+h%C3%ACnh+thang+ABCD(AB+song+song+CD).G%E1%BB%8Di+M+l%C3%A0+trung+%C4%91i%E1%BB%83m+DC,E+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AM+v%C3%A0+BD;F+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+BM+v%C3%A0+AC.++a)CMR:EF+song+song+AB.++b)T%C3%ADnh+EF,bi%E1%BA%BFt+AB=15cm;CD=24cm.++c)EF+c%E1%BA%AFt+AD,BC+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+t%E1%BA%A1i+I,K.CMR:IE=IF=FK.&id=647297
Câu trả lời của Nguyễn Thanh Thủy nha!!!