Cho tam giác ABC có AM là đường trung tuyến .N là điểm trên đoạn thẳng AM .Gọi D là giao điểm của CN và AB ,E là giao điểm
của BN và AC .CMR: AD/BD=AE/CE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

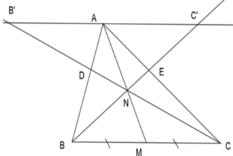
Kẻ đường thẳng đi qua A song song với BC lần lượt cắt CD và BE kéo dài tại B’ và C’.
Vì M là trung điểm BC nên BM = MC.
Vì AB’ // MC, áp dụng định lý Talet ta có: A N N M = A B ' M C (1)
Vì AC’ // BM, áp dụng định lý Talet ta có: A N N M = A C ' M B (2)
Từ (1) và (2) ta có: A B ' M C = A C ' B M
Ta có M là trung điểm BC => BM = MC => AB’ = AC’ (*)
Vì AB’ // BC, áp dụng định lý Talet ta có: A D D B = A B ' B C (**)
Vì AC’ // BC, áp dụng định lý Talet ta có: A E E C = A C ' B C (***)
Từ (*), (**) và (***) ta có:
A D D B = A B ' B C = A E E C = A C ' B C ⇒ A D D B = A E E C ⇔ A D B D = A E C E
hay DE // BC
Đáp án: C

a, Ta có:
góc DAB = góc EAC( Vì cùng phụ góc BAC)
AD= AC
AB=AE
Nên tam giác ABD = tam giác AEC
Vây BD = CEb,
Ta có: ACNB là hình bình hành nên góc ACN + góc BAC = 180độ (1)
Mặt khác ta có : 2( góc DAB +góc BAC) = 2. 90 độ = 180độ
Nên góc DAB + góc EAC + góc BAC + góc BAC = 180 độ
Suy ra DAE + BAC = 180 độ (2)
Từ (1) và (2) ta đc góc DAE = góc ACN
Mà AD = AC; AB= CN nên tam giác ADE = Tam giác cân
c, Ta có: góc NAC = góc ADE ( cmt )
Mà góc NAC + góc DAM = 90 độ nên ADE + góc DAM = 90 độ
Vậy DIA = 90 độ
Áp dụng pytago ta có:\(\frac{AD^2+IE^2}{DI^2+AE^2}=\frac{\left(AD^2+DI^2\right)+\left(AE^2-AI^2\right)}{DI^2+AE^2}=1\)
My sollution