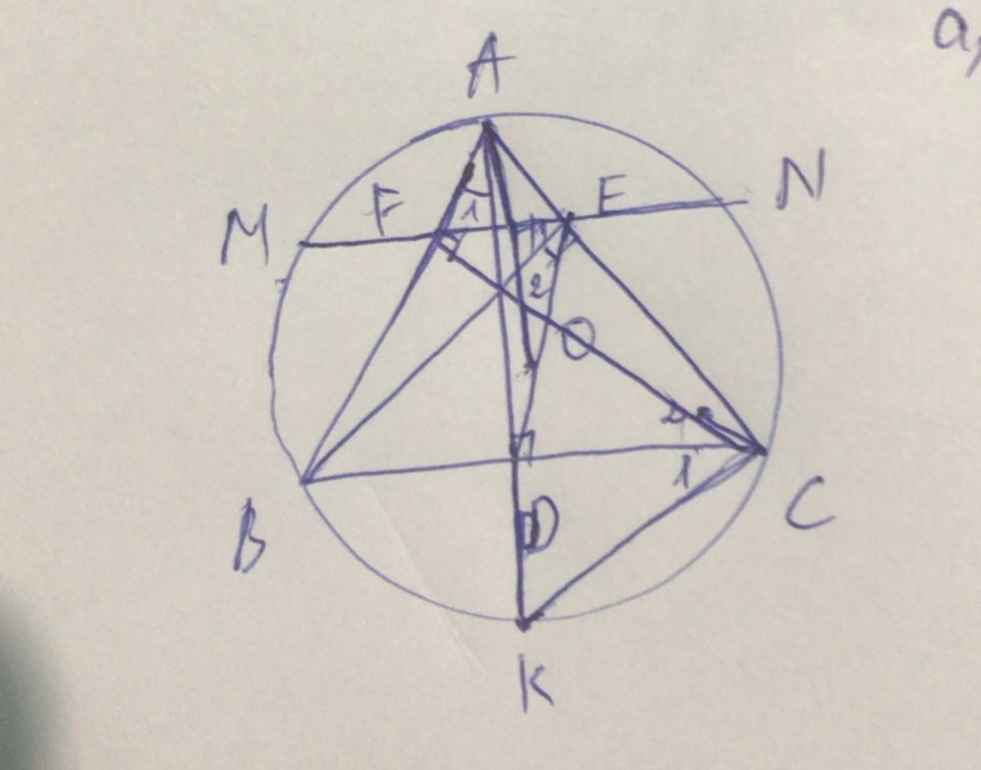
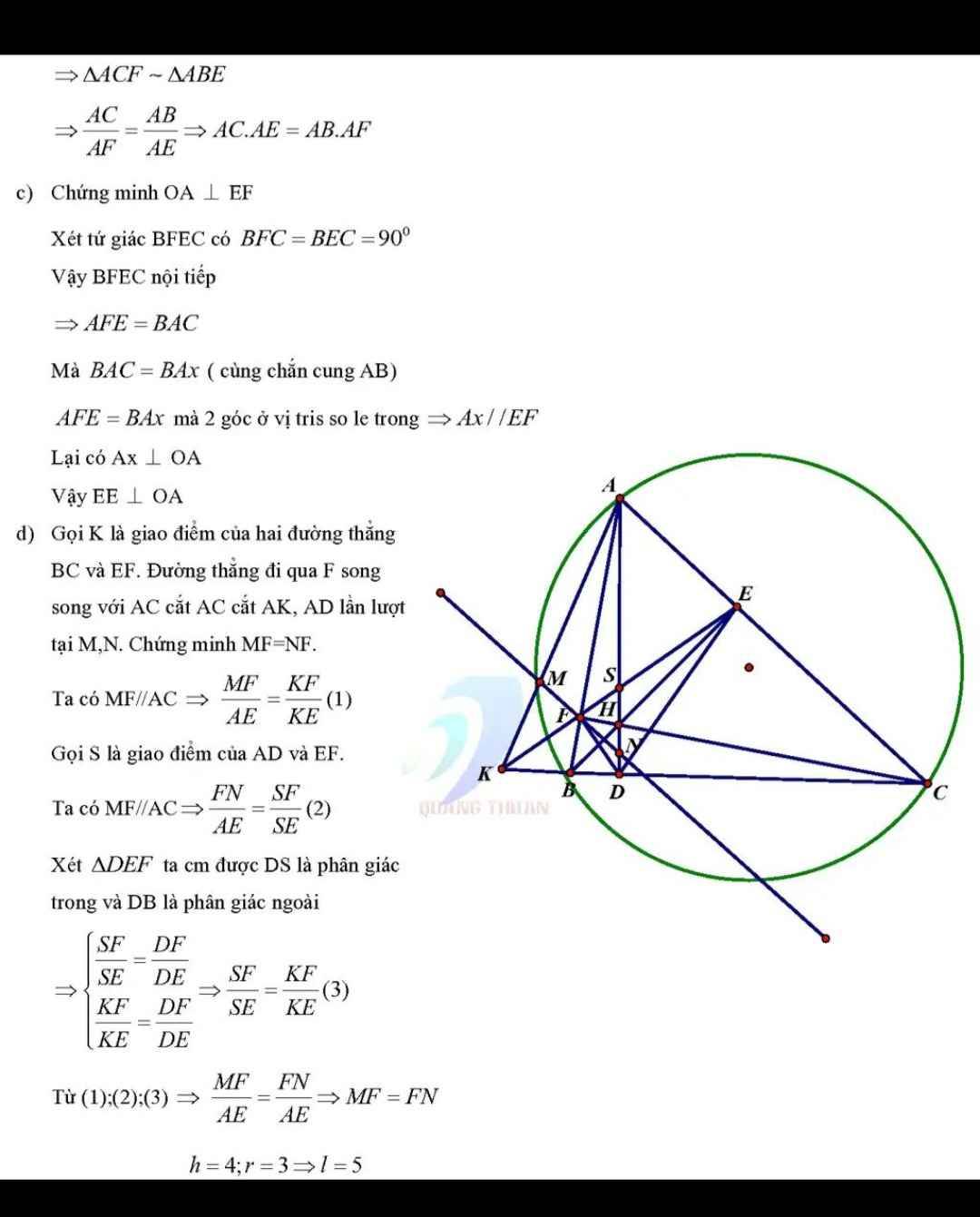
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Đường thẳng EF cắt BC tại G, đường thẳng AG cắt lại đường tròn (O) tại M.
a) Chứng minh 4 điểm A, M, E, F cùng nằm trên một đường tròn.
b) Gọi N là trung điểm của BC. Chứng minh GH vuông góc với AN.