Tam giác vuông cân tại A có CA=4,4cm. điểm M thuộc BC. D và E lần lượt là chân đường vuông góc kẻ tự M đến AB và BC. chu vi tứ giác ADME là...
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 5 2017
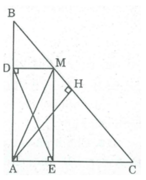
Xét tứ giác ADME, ta có:
∠ A= 90 0 (gt)
MD ⊥ AB (gt)
⇒ ∠ (ADM) = 90 0
Lại có, MD ⊥ AC ⇒ ∠ (MEA) = 90 0
Suy ra tứ giác ADME là hình chữ nhật (vì có 3 góc vuông)
∆ ABC vuông cân tại A ⇒ ∠ B = 45 0 và AB = AC = 4cm
Suy ra: ∆ DBM vuông cân tại D
⇒ DM = DB
Chu vi hình chữ nhật ADME bằng:
2(AD + DM) = 2(AD + DB) = 2AB = 2.4 = 8 (cm)
TD
6 tháng 12 2015
các bước nè
C/m tam giác DBM vuông cân tại D =>DB=DM
=>AD+DB=4cm=AD+DM
=>chu vi hcn ADME là (AD+DM)*2=4*2=8cm
bạn xem thử nhé ^_^
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 7 2023
\(MD\perp AB\) (gt)
\(AC\perp AB\) (gt)
=> MD//AC (1) \(\Rightarrow\widehat{BMD}=\widehat{C}\) (góc đồng vị)
Mà \(\widehat{B}=\widehat{C}\) (gt)
\(\Rightarrow\widehat{B}=\widehat{BMD}\) => tg BMD vuông cân tại D => MD=BD (2)
\(ME\perp AC\) (gt)
\(AB\perp AC\) (gt)
=> ME//AB (3)
C/m tương tự ta cũng có tg CME vuông cân tại E => ME=CE (4)
Từ (1) và (3) => ADME là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau)
=> MD = AE (5) và ME = AD (6)
Ta có
\(C_{ADME}=\left(MD+ME\right)x2\)
AE = AC-CE Từ (5) => MD=AC - CE Từ (4) => MD = AC - ME
\(\Rightarrow C_{ADME}=\left(AC-ME+ME\right)x2=2xAC\) không đổi
BB
8 tháng 11 2017
MDA = DAE = AEM = 90
=> ADME là hcn
Tam giác ABC vuông cân tại A
=> ACB = ABC = 45
mà MEC = 90
=> Tam giác EMC vuông cân tại E
=> EM = EC
mà DM = AE (ADME là hcn)
=> EM + DM = EC + AE = AC = 4 (cm)
PADME = 2 . (EM + DM) = 2 . 4 = 8 (cm)
DE = AM (ADME là hcn)
=> DE nhỏ nhất
<=> AM nhỏ nhất
<=> AM _I_ BC tại M
mà tam giác ABC vuông cân tại A
=> AM là đường trung tuyến
=> M là trung điểm
Vậy DE nhỏ nhất <=> M là trung điểm của BC.
30 tháng 6 2017
Ta có \(DE=AM\ge AH\). Dấu " = " xảy ra khi \(M\equiv H\)
Vậy DE có độ dài nhỏ nhất là AH khi điểm M là trung điểm của BC.