cho x,y,z là các số thực ko âm. tìm gtnn của x4+y4+z4, biết x+y+z=2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NX
1
VD
1
N
8 tháng 9 2019
Ta co:\(x^2+y^2+z^2\ge\frac{\left(x+y+z\right)^2}{3}=\frac{9}{3}=3\) ; \(xyz\le\frac{\left(x+y+z\right)^3}{27}=\frac{27}{27}=1\)
\(P=x^4+y^4+z^4+12\left(1-z-y+yz-x+xz+xy-xyz\right)\)
\(=x^4+y^4+z^4+12-12xyz-12\left(x+y+z\right)+12\left(xy+yz+zx\right)\)
\(\ge\frac{\left(x^2+y^2+z^2\right)^2}{3}+12-12.\frac{\left(x+y+z\right)^3}{27}-12.3+12\left(xy+yz+zx\right)\)
\(\ge3+12-12.1-36+4.\left(xy+yz+zx\right)\left(x+y+z\right)\)
\(\ge-33+4.\left(xy+yz+zx\right)\left(\frac{x+y+z}{xyz}\right)\)
\(=-33+4.\left(xy+yz+zx\right)\left(\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}\right)\ge-33+4\left(xy.\frac{1}{xy}+yz.\frac{1}{yz}+zx.\frac{1}{zx}\right)^2\)
\(=-33+4\left(1+1+1\right)^2=-33+36=3\)
Dau '=' xay ra khi \(x=y=z=1\)
Vay \(P_{min}=3\)khi \(x=y=z=1\)
NP
2
17 tháng 12 2020
Xét hiệu \(x^4-15x+14=\left(x-1\right)\left(x-2\right)\left(x^2+3x+7\right)\le0\)
\(\Rightarrow x^4\le15x-14\).
Tương tự: \(y^4\le15y-14;z^4\le15z-14\).
Cộng vế với vế của các bất đẳng thức trên kết hợp giả thiết x + y + z = 5 ta có:
\(P=x^4+y^4+z^4\le15\left(x+y+z\right)-42=33\).
Đẳng thức xảy ra khi và chỉ khi (x, y, z) = (2, 2, 1) và các hoán vị.
Vậy...
17 tháng 12 2020
cho mình hỏi làm thế nào để bạn tìm ra đc cách xét hiệu x4-15x+14
có phưong pháp nào ko
nếu có thì bn giúp mk vs nhé
GV
3
BT
10 tháng 3 2018
Cách 1:
Áp dụng tính chất cuẩ BĐT, Ta có: \(x^4+y^4+z^4\ge\frac{\left(x^2+y^2+z^2\right)^2}{3}\)
Lại có: \(x^2+y^2+z^2\ge\frac{\left(x+y+z\right)^2}{3}\)
=> \(x^4+y^4+z^4\ge\frac{\left(\frac{x+y+z}{3}\right)^2}{3}=\frac{16}{27}\)
=> GTNN của \(x^4+y^4+z^4=\frac{16}{27}\) đạt được khi x=y=z=2/3
HL
3
6 tháng 9 2016
\(x^4+y^4+z^4\ge\frac{\left(x^2+y^2+z^2\right)^2}{3}\ge\frac{\left[\frac{\left(x+y+z\right)^2}{3}\right]^2}{3}=\frac{\left(x+y+z\right)^4}{27}=\frac{16}{27}..\)
Min = 16/27 khi x =y =z = 2/3
6 tháng 9 2016
\(\left(x+y+z\right)^2=x^2+y^2+z^2+xy+yz+zx=2\)
mà \(xy+yz+zx\le x^2+y^2+z^2\)
\(\Rightarrow x^2+y^2+z^2\ge\frac{4}{3}\)
Tương tự:\(x^4+y^4+z^4\ge\left(x^2+y^2+z^2\right)\cdot\frac{1}{3}\ge\frac{4^2}{3^2}\cdot\frac{1}{3}=\frac{16}{27}\)
Dấu ''='' xảy ra khi x=y=z=2/3
HT
1
ND
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
13 tháng 7 2023
\(\left(x+y+z\right)^2=x^2+y^2+z^2+2xy+2yz+2xz\) Thay x+y+z=0 vào
\(\Rightarrow0=x^2+y^2+z^2+2\left(xy+yz+xz\right)\)
\(\Leftrightarrow x^2+y^2+z^2=-2\left(xy+yz+xz\right)\) (1)
Ta có
\(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+2x^2y^2+2y^2z^2+2x^2z^2\) (2)
Bình phương 2 vế của (1)
\(\left(x^2+y^2+z^2\right)^2=4\left(xy+yz+xz\right)^2\)
\(\Leftrightarrow\left(x^2+y^2+z^2\right)^2=4\left(x^2y^2+y^2z^2+x^2z^2+2xy^2z+2xyz^2+2x^2yz\right)\)
\(\Leftrightarrow\left(x^2+y^2+z^2\right)^2=4\left[x^2y^2+y^2z^2+x^2z^2+2xyz\left(x+y+z\right)\right]\)
Do x+y+z=0 nên
\(\left(x^2+y^2+z^2\right)^2=4\left(x^2y^2+y^2z^2+x^2z^2\right)\)
\(\Rightarrow\dfrac{\left(x^2+y^2+z^2\right)^2}{2}=2x^2y^2+2y^2z^2+2x^2z^2\) (3)
Thay (3) vào (2)
\(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+\dfrac{\left(x^2+y^2+z^2\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4+z^4\right)=\left(x^2+y^2+z^2\right)^2\) (đpcm)
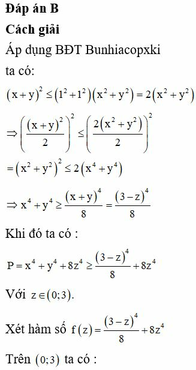
- Áp dụng bất đẳng thức cô - si ta được :
\(\frac{x^4}{4}\ge\sqrt[4]{x^4}\) => \(x^4\ge4x\)
\(\frac{y^4}{4}\ge\sqrt[4]{y^4}\)=> \(y^4\ge4y\)
\(\frac{z^4}{4}\ge\sqrt[4]{z^4}\)=> \(z^4\ge4z\)
- Cộng 3 vế bất đẳng thức trên ta được :
\(x^4+y^4+z^4\ge4\left(x+y+z\right)\)
=> \(x^4+y^4+z^4\ge8\)
Vậy GTNN của biểu thức trên là 8 .
Dấu "=" xảy ra <=> x = y = z = 1 .
à đó là căn bậc 4