Cho 2 đa thức:
p(x)=2x3 - 3x2 + x ;
q(x)=x3 - x2 +2x + 1.
Tính p(x)-2q (x) ; p(x) + 3q(x)
Giúp mk với nha!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
8 tháng 5 2022
Lời giải:
a.
\(C(x)=A(x)+B(x)=(2x^3-3x^2-x+1)+(-2x^3+3x^2+5x-2)\)
\(=(2x^3-2x^3)+(-3x^2+3x^2)+(-x+5x)+(1-2)=4x-1\)
b.
$C(x)=4x-1=0$
$\Rightarrow x=\frac{1}{4}$
Vậy $x=\frac{1}{4}$ là nghiệm của $C(x)$
c.
\(D(x)=A(x)-B(x)=(2x^3-3x^2-x+1)-(-2x^3+3x^2+5x-2)\)
\(=2x^3-3x^2-x+1+2x^3-3x^2-5x+2\)
\(=4x^3-6x^2-6x+3\)
5 tháng 8 2021
Ta có: \(P\left(x\right)⋮Q\left(x\right)\)
\(\Leftrightarrow2x^3-7x^2+5x+1⋮2x-1\)
\(\Leftrightarrow2x^3-x^2-6x^2+3x+2x-1+2⋮2x-1\)
\(\Leftrightarrow2⋮2x-1\)
\(\Leftrightarrow2x-1\in\left\{1;-1;2;-2\right\}\)
\(\Leftrightarrow2x\in\left\{2;0;3;-1\right\}\)
hay \(x\in\left\{1;0;\dfrac{3}{2};-\dfrac{1}{2}\right\}\)
6 tháng 1 2021
\(2x^3-3x^2+x+a=\left(x+2\right)\left(2x^2-7x+15\right)+\left(a-30\right)=Q\left(x\right).\left(x+2\right)\)
=> x=-2 thì \(2.\left(-2\right)^2-3\left(-2\right)^2+\left(-2\right)+a=Q\left(x\right).0=0\)
<=> -16 -12 -2 +a =0
<=> a -30 =0
=> a= 30.
PT
1
CM
28 tháng 4 2017
Thực hiện phép chia:
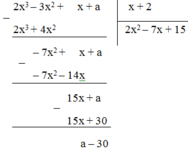
2x3 – 3x2 + x + a chia hết cho x + 2
⇔ số dư = a – 30 = 0
⇔ a = 30.
Cách 2: Phân tích 2x3 – 3x2 + x + a thành nhân tử có chứa x + 2.
2x3 – 3x2 + x + a
= 2x3 + 4x2 – 7x2 – 14x + 15x + 30 + a – 30
(Tách -3x2 = 4x2 – 7x2; x = -14x + 15x)
= 2x2(x + 2) – 7x(x + 2) + 15(x + 2) + a – 30
= (2x2 – 7x + 15)(x + 2) + a – 30
2x3 – 3x2 + x + a chia hết cho x + 2 ⇔ a – 30 = 0 ⇔ a = 30.
HG
3
A
5 tháng 8 2023
Số dư của phép chia đa thức \(\text{f( x ) = 2x^3 - 3x^2 + x + a}\) cho \(\text{x + 2}\) là
\(\text{f ( -2 ) = 2(-2) ^3 - 3 (-2 )^2 + ( - 2 ) + a = -30 + a}\)
Để phép chia là chia hết thì số dư bằng \(\text{0}\)
Hay \(\text{-30 + a = 0}\) \(\Rightarrow\) \(\text{a = 30}\)
15 tháng 7 2021
a)P(x) = 7x3 - x2 + 5x - 2x3 +6 - 8x
=5x^3-x^2-3x+6
Q(x) = -2x + x3 - 4x2 + 3 - 5x2
=x^3-9x^2-2x+3
b)
P(x) - Q(x)=4^3+8x^2-x-3
P(x) + Q(x)=6^3-10x^2-5x+9
VT
2
KT
9 tháng 5 2018
Đa thức \(f\left(x\right)=2x^3-3x^2+x+a\) chia hết cho đa thức \(x+2\)
\(\Leftrightarrow\)\(f\left(-2\right)=0\)
\(\Leftrightarrow\)\(2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a=0\)
\(\Leftrightarrow\)\(-30+a=0\)
\(\Leftrightarrow\)\(a=30\)
Vậy \(a=30\)thì \(2x^3-3x^2+x+a\)chia hết cho \(x+2\)
p/s: bn có thế lm theo cách truyền thống: đặt tính chia ra rồi đặt dư = 0 và tìm a
hoặc dùng hệ số bất định
9 tháng 5 2018
2x^3-3x^2+x+a | x+2
------------------|-------------
2x^3-3x^2 | 2x^2-7x+15
2x^2+4x^2
-7x^2+x
-7x^2-14x
15x+a
15x+30
\(2x^3-3x^2+x+a\div x+2\)
Để đa thức \(2x^3+3x^2+x+a⋮x+2\)
\(\Rightarrow15x+a=15x+30\)
\(\Rightarrow a-30=0\Rightarrow a=30\)
CM
11 tháng 2 2019
Đặt và thực hiện phép tính ta có :
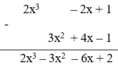
Vậy chọn đa thức thứ hai.