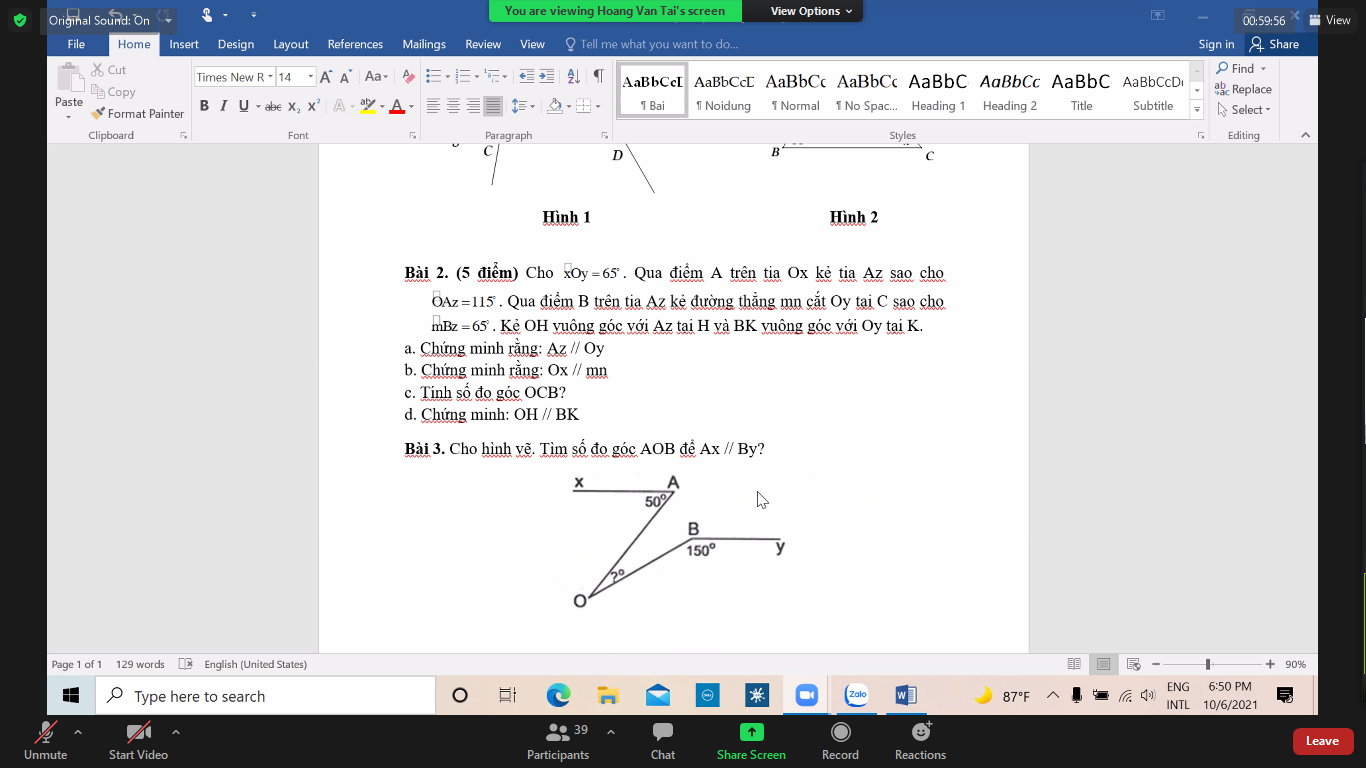
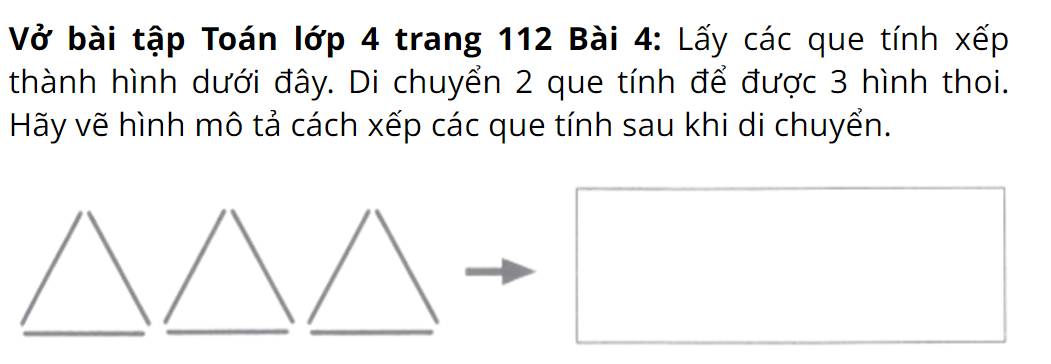
Giúp em bài 3 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 10 2021
Giả sử Ax//By
Kẻ Ax//By//Oz
\(\Rightarrow\widehat{OAx}=\widehat{AOz}=50^0\)(so le trong)
Ta có: By//Oz
\(\Rightarrow\widehat{OBy}+\widehat{BOz}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{OBz}=180^0-150^0=30^0\)
Ta có: \(\widehat{AOB}=\widehat{AOz}-\widehat{BOz}=50^0-30^0=20^0\)
\(\Rightarrow x=20^0\)
11 tháng 8 2021
5
\(=>\dfrac{R1}{R2}=\dfrac{S2}{S1}=\dfrac{4S1}{S1}=4=>R1=4R2\)
R1//R2\(=>U1=U2=>I1.R1=I2.R2=>4.4R2=I2.R2\)
\(=>16=I2=>I2=16A\)
11 tháng 8 2021
6.
ta chọn dây dẫn thứ 3 bằng nhôm có chiều dài l3=l1
và S3=S2
\(=>\dfrac{R1}{R3}=\dfrac{S3}{S1}=>\dfrac{5,6}{R3}=\dfrac{1.10^{-6}}{0,5.10^{-6}}=>R3=2,8\left(ôm\right)\)
chọn dây dẫn R3 có tiết diện S3=S2 và l3=l1
\(=>\dfrac{R3}{R2}=\dfrac{l3}{l2}=>\dfrac{2,8}{16,8}=\dfrac{100}{l2}=>l2=600m\)
1 tháng 9 2021
a: Ta có: \(2\sqrt{28}+3\sqrt{63}-3\sqrt{\dfrac{112}{9}}-\sqrt{\dfrac{196}{7}}\)
\(=4\sqrt{7}+9\sqrt{7}-4\sqrt{7}-2\sqrt{7}\)
\(=7\sqrt{7}\)
b: Ta có: \(\sqrt{8+2\sqrt{7}}-\sqrt{12-\sqrt{140}}-\sqrt{5}\)
\(=\sqrt{7}+1-\sqrt{7}+\sqrt{5}-\sqrt{5}\)
=1
MM
1
MM
1
20 tháng 12 2021
Câu 1:
\(a,=4\sqrt{3}-10\sqrt{3}+8\sqrt{3}=2\sqrt{3}\\ b,=3-\sqrt{5}+\sqrt{5}-1=2\)
Câu 2:
\(a,ĐK:x\ge-2\\ PT\Leftrightarrow4\sqrt{x+2}-3\sqrt{x+2}+\sqrt{x+2}=6\\ \Leftrightarrow\sqrt{x+2}=3\Leftrightarrow x+2=9\Leftrightarrow x=7\left(tm\right)\\ b,\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\5y=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=3\end{matrix}\right.\)
Câu 3:
\(b,PTHDGD:2x-3=-x+3\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ c,\Leftrightarrow A\left(2;1\right)\in\left(d_3\right)\Leftrightarrow2m-6+m=1\Leftrightarrow m=\dfrac{7}{3}\)
TT
3
15 tháng 9 2021
a) \(A=\dfrac{x+\sqrt{xy}}{y+\sqrt{xy}}=\dfrac{\sqrt{x}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{x}}{\sqrt{y}}\)
b) \(B=\dfrac{\sqrt{a}+a\sqrt{b}-\sqrt{b}-b\sqrt{a}}{ab-1}=\dfrac{\sqrt{a}\left(1+\sqrt{ab}\right)-\sqrt{b}\left(1+\sqrt{ab}\right)}{\left(\sqrt{ab}-1\right)\left(1+\sqrt{ab}\right)}=\dfrac{\left(1+\sqrt{ab}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}-1}=\dfrac{\sqrt{a}-\sqrt{b}}{\sqrt{ab}-1}\)
15 tháng 9 2021
c) \(C=\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}=\dfrac{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}+x\right)}{1+\sqrt{x}}=1-\sqrt{x}+x\)
d) \(D=\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}-x+2\sqrt{xy}-y=x-\sqrt{xy}+y-x+2\sqrt{xy}-y=\sqrt{xy}\)
e) \(\dfrac{x+4\sqrt{x}+4}{\sqrt{x}+2}+\dfrac{4-x}{2-\sqrt{x}}=\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}+2}+\dfrac{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}{2-\sqrt{x}}=\sqrt{x}+2+2+\sqrt{x}=2\sqrt{x}+4\)
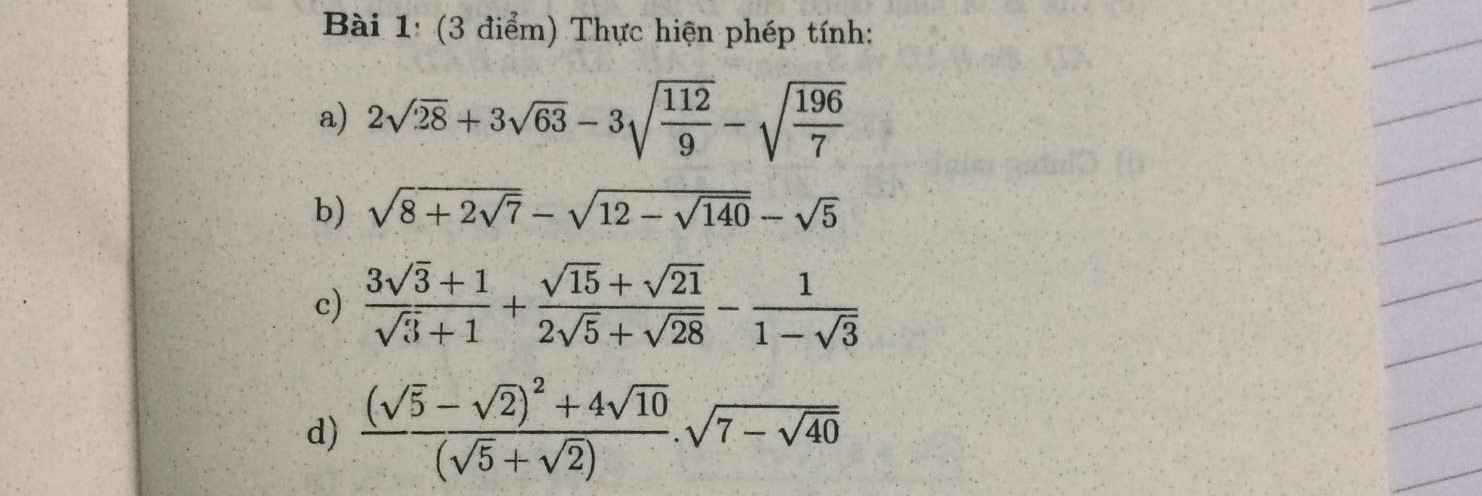
Mai em học bài này nhg e ch nghĩ ra