Cho 2x = 8y+1 và 9y = 3x-9 với x, y là các số tự nhiên . Hãy tính x+y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2x = 8y+1
<=> 2x = 23.(y+1)
<=> x = 3.(y+1) <=> x = 3y + 3(1)
9y = 3x-9 <=> 2y = x - 9.(2)
(1)-(2) vtv => x - x + 9 = 3y + 3 - 2y
<=> 6 = y => x = 3.6 + 3 = 21
vậy x+y = 27

Để tìm các số tự nhiên x và y thỏa mãn phương trình (2x - 9)/(x - 2) + 1 = y, ta sẽ giải phương trình này.
Bước 1: Loại bỏ phân số trong phương trình bằng cách nhân cả hai vế của phương trình với (x - 2):
(x - 2) * [(2x - 9)/(x - 2) + 1] = y * (x - 2)
Bước 2: Rút gọn phân số và thu gọn phương trình:
2x - 9 + (x - 2) = y * (x - 2)
3x - 11 = y * (x - 2)
Bước 3: Giải phương trình để tìm x và y. Để làm điều này, chúng ta có thể thử các giá trị của x và kiểm tra các giá trị tương ứng của y. Dựa trên tính chất của phương trình, chúng ta có thể thấy rằng x phải lớn hơn 2, vì nếu x = 2, mẫu số sẽ bằng 0, gây ra một phép chia không hợp lệ.
Thử x = 3:
3 * 3 - 11 = y * (3 - 2) y = 2
Vậy, một cặp số tự nhiên thỏa mãn phương trình là x = 3 và y = 2.
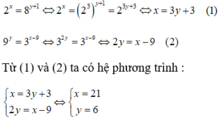
2x = 8y+1 = 23.(y+1) suy ra x = 3y+3 (1)
9y = 3x-9 suy ra 32y= 3x-9 suy ra 2y = x - 9 hay x = 2y + 9 (2)
Từ (1) và (2) suy ra 3y +3 = 2y +9
suy ra y = 6
x = 2.6 + 9 = 21
Vậy x+y = 21+6=27
\(\hept{\begin{cases}2^x=8y+1&9^y=3^{x-9}&\end{cases}=>\hept{\begin{cases}2^x=2^{3(y+1)}\\3^{2y}=3^{x-9}\end{cases}=>\hept{\begin{cases}x=3y+3\\2y=x-9\end{cases}}}=>\hept{\begin{cases}x=3y+3\left(1\right)\\x=2y+9\left(2\right)\end{cases}}}\)
Lấy 1 trừ 2 ta được : 3y+3-2y-9=0
=> y=6
thay y=6 zô (1)
ta được x=21
zậy x+y=21+6=27