chứng minh rằng |a+(1/a)| ≥ 2 với mọi a khác 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ta có: \(\frac{2a+1}{2a^2+2a}=\frac{2a+1}{2a\left(a+1\right)}\)
nhận xét: 2a và 2a +1 là 2 số nguyên liên tiếp nên 2a và 2a + 1 không có ước chung nào khác 1; -1 (*)
gọi d = ƯCLN(2a+1; a+1)
=> 2a+1 chia hết cho d và
a+ 1 chia hết cho d
=> 2a+ 1 - 2(a+1) = -1 chia hết cho d => d = 1 hoặc -1 => 2a+ 1 và a+ 1 nguyên tố cùng nhau hay chúng ko có ước chung nào khác 1; -1 (**)
Từ (*)(**) => 2a + 1 và 2a.(a+ 1) nguyên tố cùng nhau => phân số đã cho là tối giản

Điều kiện x ≠ 1 và x ≠ - 1
Ta có:

Biểu thức dương khi x 2 + 2 x + 3 > 0
Ta có: x 2 + 2 x + 3 = x 2 + 2 x + 1 + 2 = x + 1 2 + 2 > 0 với mọi giá trị của x.
Vậy giá trị của biểu thức dương với mọi giá trị x ≠ 1 và x ≠ - 1

Điều kiện x ≠ 0 và x ≠ -3
Ta có:
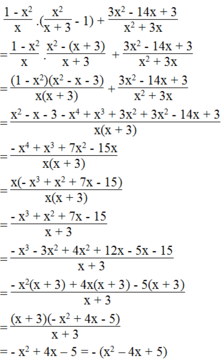
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3

Đặt \(P=a^2+b^2+\left(\frac{1+ab}{a+b}\right)^2\), ta được:
\(P=\left(a+b\right)^2+\left(\frac{1+ab}{a+b}\right)^2-2ab\)
Áp dụng bất đẳng thức Cô-si với bộ \(\left(a+b\right)^2\) và \(\left(\frac{1+ab}{a+b}\right)^2\), ta có:
\(P=\left(a+b\right)^2+\left(\frac{1+ab}{a+b}\right)^2-2ab\ge2\sqrt{\left(a+b\right)^2\left(\frac{1+ab}{a+b}\right)^2}-2ab=2\left(1+ab\right)-2ab=2\)

giúp mình nha chiều nay mình phải nộp cho thầy giáo rồi. 3 bài minh vừa mới gửi đó.
chúc các bạn có ngày cá tháng tư vui vẻ!

ta lấy vế trái nhân vs -1
ta có: \(\frac{a}{b}=\frac{a.\left(-1\right)}{b.\left(-1\right)}=\frac{-a}{-b}\)
vậy a/b = -a/-b
ta lại có: \(\frac{-a}{b}=\frac{-a.\left(-1\right)}{b.\left(-1\right)}=\frac{a}{-b}\)
vậy -a/b = a/-b
t i c k nhé!! 5756756845745756
Do \(a\) và \(\frac{1}{a}\) luôn cùng dấu
\(\Rightarrow\left|a+\frac{1}{a}\right|=\left|a\right|+\frac{1}{\left|a\right|}\ge2\sqrt{\frac{\left|a\right|}{\left|a\right|}}=2\)
Dấu "=" xảy ra khi \(a=\pm1\)