Giải giúp mình câu này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....

\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên


a) \(d\left(A;\Delta\right)=\dfrac{\left|4.1-3.3+2\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{3}{5}\)
b) \(\overrightarrow{AB}=\left(-3;-2\right)\) là VTCP của đường thẳng d
PT tham số của d: \(\left\{{}\begin{matrix}x=1-3t\\y=3-2t\end{matrix}\right.\left(t\in R\right)\)
c) Đường tròn (C) có bán kính \(R=AB=\sqrt{\left(1+2\right)^2+\left(3-1\right)^2}=\sqrt{13}\)
PT đường tròn (C): \(\left(x-1\right)^2+\left(y-3\right)^2=13\)


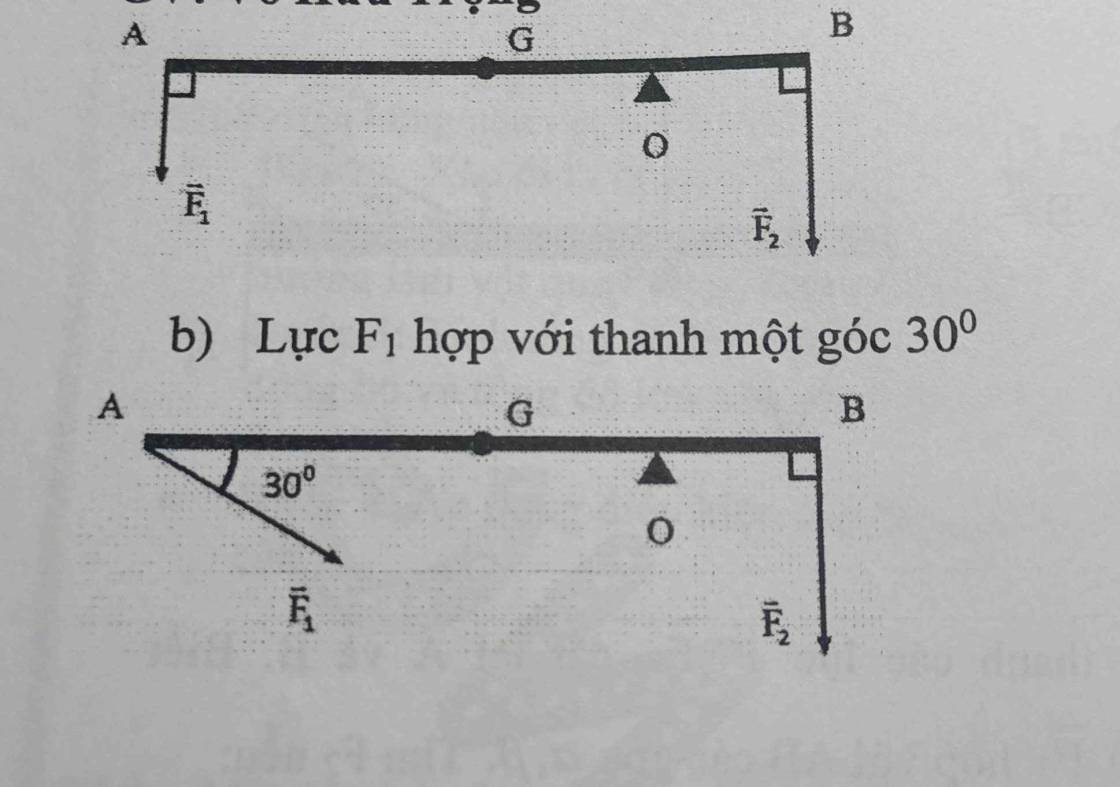
a) AD đk cân bằng momen ta có
`F_1 *OA + P*GO = OB*F_2`
`<=> F_1 *(AB-OB) + mg(AB-OB - AB/2) = OB *F_2`
`<=> F_1 (120 - 30) + 2*10*(120 - 30 -120/2) = 30*50`
`=> F_1 = 10N`
b) AD đk cân bằng momen ta có
`F_1 * sin30^o *OA + P*GO = OB*F_2`
`<=> F_1 *sin30^o *(AB-OB) + mg(AB-OB - AB/2) = OB *F_2`
`<=> F_1*sin30^o * (120 - 30) + 2*10*(120 - 30 -120/2) = 30*50`
`=> F_1 = 20(N)`


\(x^2-4x+1=0\)
\(\text{Δ}=\left(-4\right)^2-4\cdot1\cdot1=16-4=12>0\)
=>Phương trình có hai nghiệm phân biệt
\(x_1+x_2=-\left(-4\right)=4;x_1\cdot x_2=1\)
\(S=x_1^2\left(x_1-x_2\right)+x_2^2\left(x_2-x_1\right)\)
\(=x_1^2\left(x_1-x_2\right)-x_2^2\left(x_1-x_2\right)\)
\(=\left(x_1-x_2\right)\left(x_1^2-x_2^2\right)\)
\(=\left(x_1+x_2\right)\left(x_1-x_2\right)^2\)
\(=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-4x_1x_2\right]\)
\(=4\cdot\left[4^2-4\cdot1\right]\)
\(=4\cdot\left(16-4\right)=4\cdot12=48\)






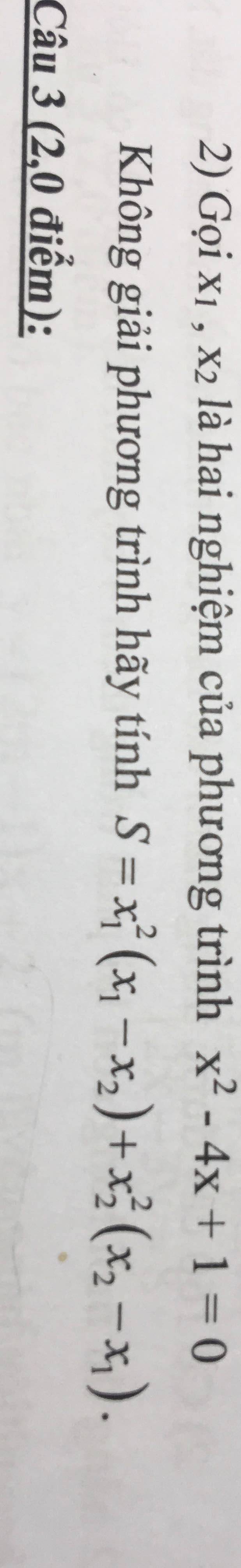
B
B