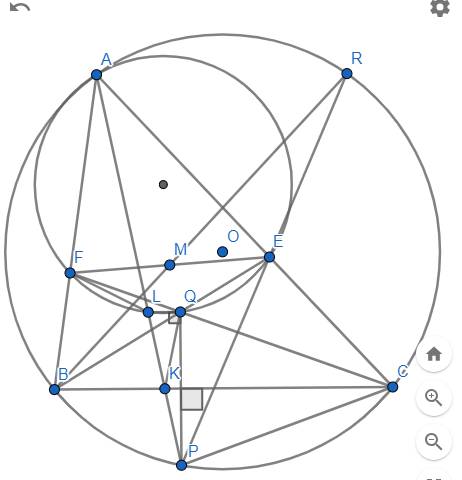
Cho tam giác ABC nội tiếp (O). (AB>AC). F là điểm chính giữa cung BC nhỏ. AF cắt BC tại D. AK là phân giác ngoài ( K thuộc tia BC ). AD=AK..
a,\(\widehat{ADK}=?\)
b, Tính \(sđ\stackrel\frown{AC}+sđ\stackrel\frown{BF}\)
c, Chứng minh : \(AB^2+AC^2=4R^2\)