10. Tính độ dài x trên hình dưới đây.11. Tính độ dài x trên hình dưới đây.12. Tính độ dài x trên các hình sau:13.* Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC) Biết HB = 9cm, HC = 16cm. Tính độ dài AH.14. Trên mặt phẳng tạo độ Oxy, vẽ điểm A có tọa độ (3;5). Tính khoảng cách từ điểm A đến gốc tọa độ.15. Trên mặt phẳng tọa độ Oxy, sẽ điểm A có tọa độ (1;1). Đường...
Đọc tiếp
10. Tính độ dài x trên hình dưới đây.
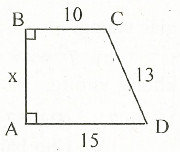
11. Tính độ dài x trên hình dưới đây.
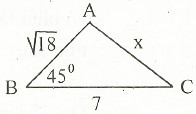
12. Tính độ dài x trên các hình sau:
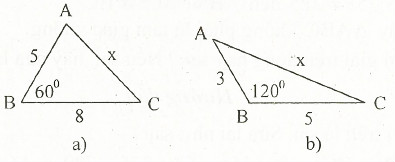
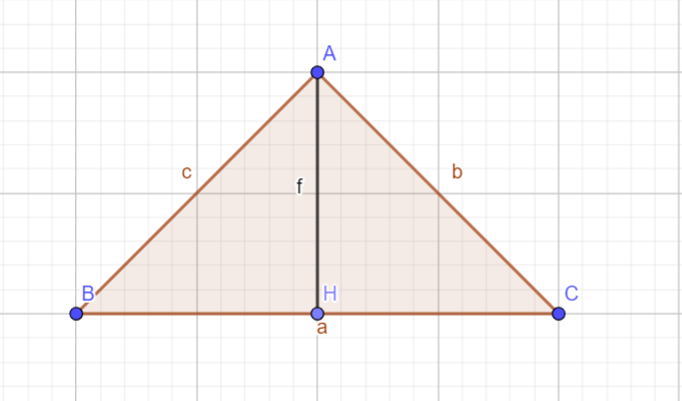
13.* Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC) Biết HB = 9cm, HC = 16cm. Tính độ dài AH.
14. Trên mặt phẳng tạo độ Oxy, vẽ điểm A có tọa độ (3;5). Tính khoảng cách từ điểm A đến gốc tọa độ.
15. Trên mặt phẳng tọa độ Oxy, sẽ điểm A có tọa độ (1;1). Đường tròn tâm O với bán kinh Oa cắt các tia Ox, Oy theo thứ tự B và C. Tìm tọa độ của các điểm B, C.
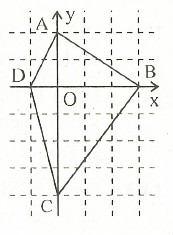
16. Tính độ dài của các đoạn thẳng AB, BC, CD, CD trên mặt phẳng tọa độ (Hình vẽ bên, với đơn vị là đơn vị dài của hệ trục tọa độ).
MN GIÚP MK VS ....MK ĐANG CẦN RẤT GẤP, AI BIẾT GIẢI BÀI NÀO THÌ GIẢI CHI TIẾT ĐẦY ĐỦ GIÚP MK VS
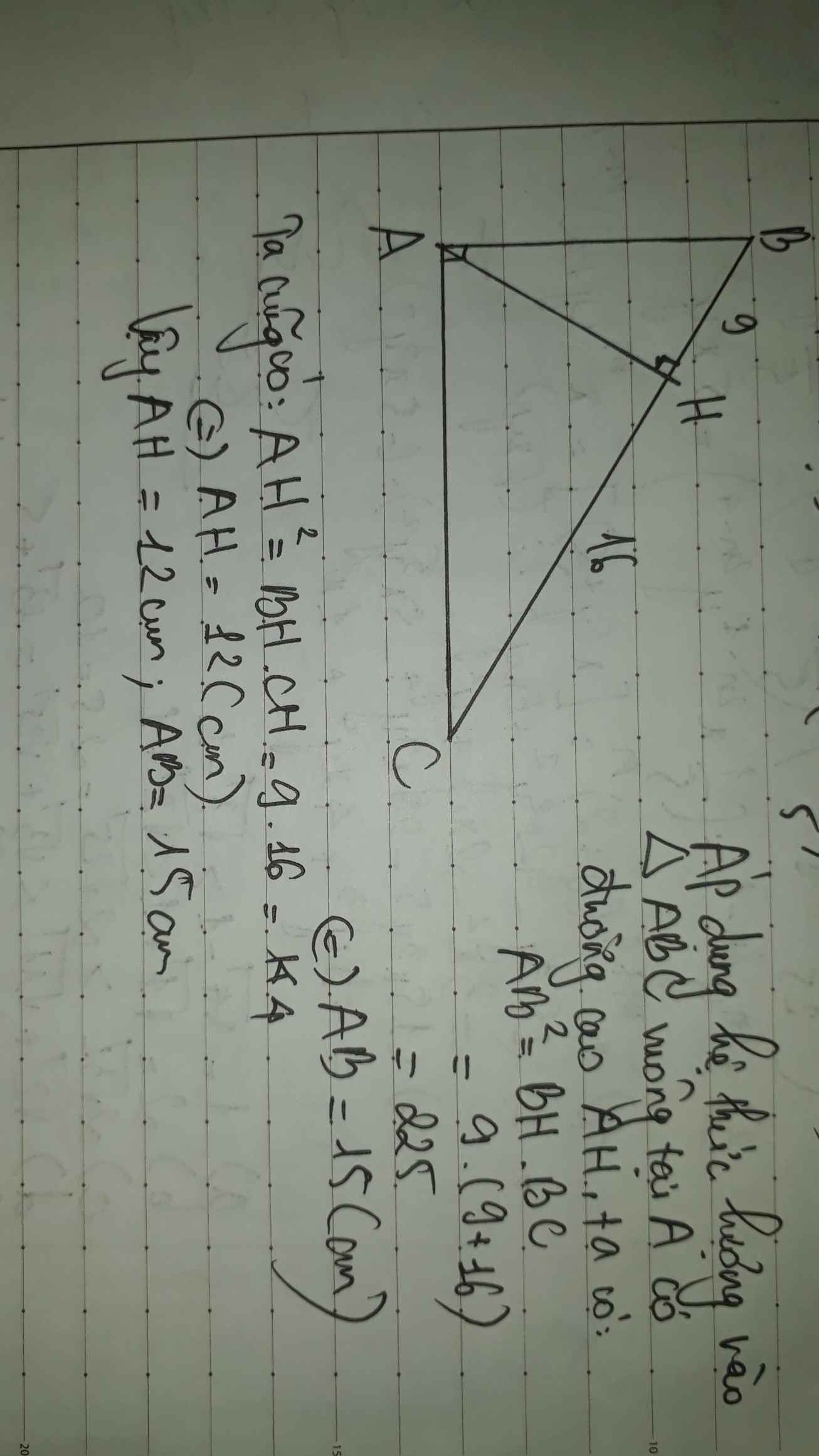
10.
11.
12.
15.
HÌNH ĐÂY NHA MN...
lj có hình nào bn