Điểm di động là gì?
Và khi vẽ điểm di động trên một cạnh thì vẽ như thế nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


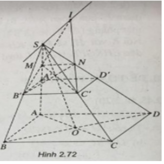
a) (P) // BC nên (P) sẽ cắt (SBC) theo giao tuyến B'C' song song với BC.
Tương tự, (P) cắt (SAD) theo giao tuyến MN song song với AD.
Khi M trùng với trung điểm A' của cạnh SA thì thiết diện MB'C'N' là hình bình hành.
b) Với M không trùng với A':
Gọi I ∈ B′M ∩ C′N. Ta có:
I ∈ B′M ⊂ (SAB), tương tự I′ ∈ C′N ⊂ (SCD)
Như vậy I ∈ Δ = (SAB) ∩ (SCD).

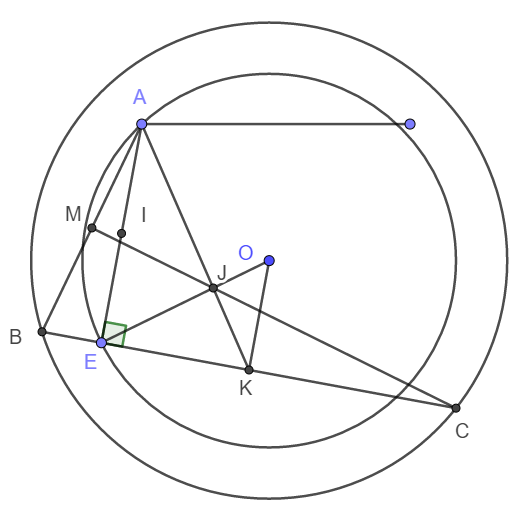
a) Gọi I, K lần lượt là trung điểm của AE và BC.
Ta có : \(EB^2=\left(BK-EK\right)^2;EC^2=\left(KC+EK\right)^2\)
\(\Rightarrow EB^2+EC^2=2\left(BK^2+EK^2\right)=2\left(BO^2-OK^2+OE^2-OK^2\right)\)
\(=2\left(R^2+r^2\right)-4OK^2\)
\(AE^2=4AI^2=4\left(r^2-OI^2\right)\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+6r^2-4\left(OI^2+OK^2\right)\)
Mà OIEK là hình chữ nhật nên \(OI^2+OK^2=OE^2=r^2\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+2r^2\) không đổi.
b) Giả sử EO giao với AK tại J.
Vì IOEK là hình chữ nhật nên OK song song và bằng EI. Vậy nên OK song song và bằng một nửa AE.
Do đó \(\frac{JE}{JO}=\frac{AJ}{JK}=\frac{AE}{OK}=2\)
Vì OE cố định nên J cố định; Vì AK là trung tuyến của tam giác ABC nên J là trọng tâm tam giác ABC
Suy ra J thuộc MC.
Vậy MC đi qua J cố định.
c) Vì AK = 3/2AJ nên H trùng K.
Do đó OH vuông góc BC. Suy ra H thuộc đường tròn đường kính OE.

Bạn tự vẽ hình
1. Gọi \(K\) là điểm chính giữa của nửa đường tròn. Xét hai tam giác \(\Delta KOD\) và \(\Delta OCH\) có \(OK=CO=R\), \(\angle KOD=\angle OCH\) (so le trong) và \(OD=CH\) (giả thiết). Suy ra hai tam giác \(\Delta KOD\) và \(\Delta OCH\)
bằng nhau (c.g.c). Do đó \(\angle KDO=90^{\circ}\to D\) nằm trên đường tròn đường kính OK.
Khi C trùng A thì D trùng với O và khi C trùng với B thì D trùng với O. Do đó tập hợp D sẽ là toàn bộ đường tròn đường kính OK.
2. Kéo dài tia DC cắt (O) ở điểm thứ hai T. Do tứ giác ACTB nội tiếp nên góc TBA = góc DCA = 60 độ. Vậy T là điểm cố định. Do tam giác ACD đều và M là trung điểm CD nên AM vuông góc với CD. Suy ra M nhìn đoạn AT dưới 1 góc vuông. Vậy M nằm trên đường tròn đường kính AT.
Vì C chỉ chạy trên nửa đường tròn, khi C trùng A thì M trùng A và khi C trùng với B thì M trùng với T. Vậy M chạy trên nửa đường tròn đường kính AT, trong nửa mặt phẳng không chứa điểm B.
Chỉ vậy thôi.

Giải
Ta có nhận xét: tổng độ dài hai cạnh của hai hình vuông bằng AB là độ dài không đổi.
Từ O, M, O' hạ các đường vuông góc với AB như hình vẽ.
Ta có: OX bằng nửa cạnh hình vuông AICD; O'Y bằng nửa cạnh hình vuông BIEF.
=> OX + OY = 1/2 AB là đại lượng không đổi
MZ là đường trung bình của hình thang O'YXO
=> MZ = 1/2 (OX + OY) = 1/2 . 1/2 AB = 1/4 AB
Suy ra khoảnh cách từ M đến AB là đại lượng không đổi ( = 1/4 AB).
Vậy M nằm trên đường thẳng song song với AB và cách AB bằng độ dài bằng 1/4 AB

Ta có nhận xét: tổng độ dài hai cạnh của hai hình vuông bằng AB là độ dài không đổi.
Từ O, M, O' hạ các đường vuông góc với AB như hình vẽ.
Ta có: OX bằng nửa cạnh hình vuông AICD; O'Y bằng nửa cạnh hình vuông BIEF.
=> OX + OY = 1/2 AB là đại lượng không đổi
MZ là đường trung bình của hình thang O'YXO
=> MZ = 1/2 (OX + OY) = 1/2 . 1/2 AB = 1/4 AB
Suy ra khoảnh cách từ M đến AB là đại lượng không đổi ( = 1/4 AB).
Vậy M nằm trên đường thẳng song song với AB và cách AB bằng độ dài bằng 1/4 AB
đáp án là M nằm trên đường thẳng song song với AB và cách AB bằng độ dài bằng 1/4 AB