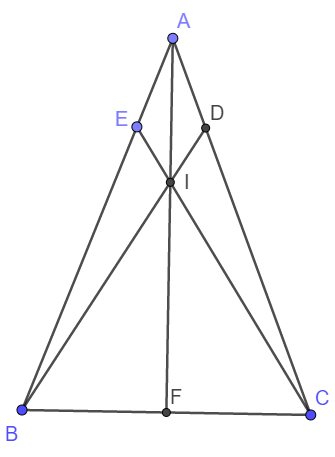
Cho taam giác ABC có AB=AC. TRên cạnh AB lấy điểm E, trên cạnh AC lấy điểm D sao cho AE=AD. Gọi I là giao điểm của BD và CE, F là trung điểm của BC. Chứng minh rằng:
a) BD = CE
b) Tam giác CEB = tam giác BDC
c) Tam giác BIE = tam giác CID
d) Ba điểm A, I, F thẳng hàng
(có thể cho mình xin hình nữa nhé !)

Bài này easy lắm bạn
a) Xét \(\Delta\) ABD và \(\Delta\)ACE có
AB = AC ( gt)
\(\widehat{BAC}\) : góc chung
AD = AE ( gt)
=> \(\Delta\)ABD = \(\Delta\) ACE (c-g-c)
=> BD = CE ( 2 cạnh tương ứng )
+) Ta có \(\hept{\begin{cases}AB=AC\left(gt\right)\\AE=AD\left(cmt\right)\end{cases}}\)
\(\Rightarrow AB-AE=AC-AD\)
\(\Rightarrow\)BE = CD
+) Xét \(\Delta\)CEB và \(\Delta\)BDC có
CE = BD ( cmt)
EB = DC ( cmt)
CB: cạnh chung
=> \(\Delta\)CEB = \(\Delta\) BDC (c-c-c)
2 câu này đã nhé