Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔADB và ΔAEC có:
AB=AC(gt)
A: chung
AD=AE(gt)
=>ΔADB=ΔAEC(c.g.c)
=>đpcm
b) Có: AB=AC
=>ΔABC cân ở A
=>ABC=ACB(t/c Δ cân)
=>ABD+DBC=ACE+ECB
Mà ABD=ACE(ΔADB=ΔAEC)
=>DBC=ECB
=>ΔBCF cân ở F
=>BF=CF(t/c Δ cân)
c) Ta có:
AB=AE+EB
AC=AD+DC
Mà AB=AC; AE=AD
=>EB=DC
Xét ΔEBC và ΔDCB có:
EB=DC(cmt)
EBC=DCB(ΔABC cân)
BC: chung
=>ΔEBC=ΔDCB(c.g.c)
=>CEB=BDC(hai cạnh tương ứng)
Mà AEC+BEC=ADB+CDB=180°
=>AEC=ADB
Ta có:
EC=EF+FC
BD=BF+FD
Mà EC=BD(ΔEBC=ΔDCB); BF=CF(cmt)
=>FE=FD
Xét ΔAFE và ΔAFD có:
AE=AD(gt)
AEF=ADF(cmt)
FE=FD(cmt)
=>ΔAFE=ΔAFD(c.g.c)
=>EAF=DAF(hai góc tương ứng)
=>AF là pg BAC(1)
Xét ΔHAB và ΔHAC có:
ABH=ACHF(ΔABC cân)
HB=HC(H là trđ BC)
BAH=CAH(cmt)
=>ΔHAB=ΔHAC(g.c.g)
=>BAH=CAH(hai góc tương ứng)
=>AH là pg BAC(2)
Từ (1) và (2)
=>A, F, H thuộc thẳng hàng

a, Xét Δ ADB và Δ AEC có :
AE = AD ( gt )
AB = AC ( gt )
\(\widehat{A}\) là góc chung
=> Δ ADB = Δ AEC ( c - g -c )
b, Do Δ ABD = Δ AEC (cm trên )
=> BF = CF ( hai cạnh tương ứng )
c, DO Δ ABD = Δ AEC (cm trên )
=> \(\widehat{BAF} = \widehat{CAF}\) ( hai góc tương ứng )
=> AH là tia phân giác \(\widehat{BAC}\)
Xét Δ BFH và Δ CFH có :
FH là cạnh chung
BF = CF ( cm trên )
BH = CH ( do H là trung điểm BC)
=> Δ BFH = Δ CFH ( c - c - c )
=> \(\widehat{BFH} = \widehat{CFH}\) ( hai góc tương ứng )
=> AH là tia phân giác \(\widehat{BFH}\)
mà AH cũng là tia phân giác \(\widehat{BAC}\) ( cm trên )
=> ba điểm A,F,H thẳng hàng

a) Xét tam giác ADB và AEC có:
AD = AE (gt)
AB = AC (gt)
Góc A chung
\(\Rightarrow\Delta ADB=\Delta AEC\left(c-g-c\right)\Rightarrow BD=CE\)
b) Do AB = AC; AD = AE nên BE = DC
Xét tam giác CEB và BDC có:
CE = BD (cma)
Cạnh BC chung
BC = CD (cmt)
\(\Rightarrow\Delta CEB=\Delta BDC\left(c-c-c\right)\)
c) Do \(\Delta ADB=\Delta AEC\Rightarrow\widehat{EBI}=\widehat{DCI}\)
Do \(\Delta CEB=\Delta BDC\Rightarrow\widehat{BEI}=\widehat{CDI}\)
Xét tam giác BIE và tam giác CID có:
\(\widehat{EBI}=\widehat{DCI}\)
\(\widehat{BEI}=\widehat{CDI}\)
BE = CD
\(\Rightarrow\Delta BIE=\Delta CID\left(g-c-g\right)\)
d) Do \(\Delta BIE=\Delta CID\Rightarrow IB=IC\)
Lại có AB = AC nên IA là trung trực của BC
Vậy IA đi qua trung điểm F của BC hay A, I, F thẳng hàng.

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath

Bài này easy lắm bạn
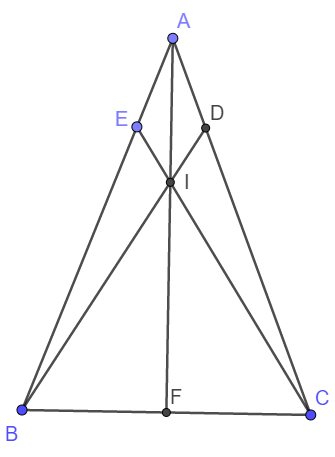
B A C D E F I Hình ảnh chỉ mang tính chất minh họa
a) Xét \(\Delta\) ABD và \(\Delta\)ACE có
AB = AC ( gt)
\(\widehat{BAC}\) : góc chung
AD = AE ( gt)
=> \(\Delta\)ABD = \(\Delta\) ACE (c-g-c)
=> BD = CE ( 2 cạnh tương ứng )
+) Ta có \(\hept{\begin{cases}AB=AC\left(gt\right)\\AE=AD\left(cmt\right)\end{cases}}\)
\(\Rightarrow AB-AE=AC-AD\)
\(\Rightarrow\)BE = CD
+) Xét \(\Delta\)CEB và \(\Delta\)BDC có
CE = BD ( cmt)
EB = DC ( cmt)
CB: cạnh chung
=> \(\Delta\)CEB = \(\Delta\) BDC (c-c-c)
2 câu này đã nhé