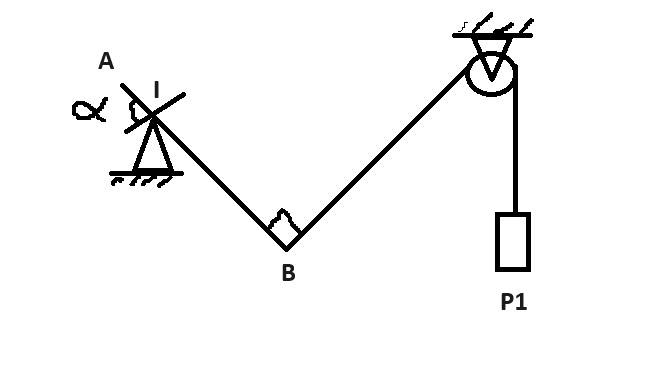
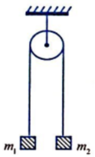
cho cơ hệ như hình vẽ thanh OA đồng chất tiết diện đều , khối lượng M , có thể tự quay quanh trục O cố định . Đầu A của thanh nối với một vật khối lượng m bằng dây nhẹ AB vắt qua ròng rọc cố định B . Biết OB nằm ngang và OA =OB . Khi hệ ở trạng thái cân bằng α = 60 độ . Tình tỷ số m/M
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
16 tháng 7 2018
Đáp án C
- Vì thanh nhẹ có thể quay quanh điểm O nên ta coi O là điểm tựa của đòn bẩy.
- Để hệ thống cân bằng ta có điều kiện cân bằng đòn bẩy như sau:
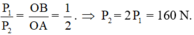
- Khối lượng vậy treo vào đầu B là:
160 : 10 = 16 (kg)
19 tháng 4 2022
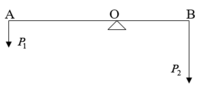
Quy tắc momen ngẫu lực:
\(M_A=M_B\Rightarrow OA\cdot F_A=OB\cdot F_B\)
\(\Rightarrow2OB\cdot m_1=OB\cdot m_2\Rightarrow2m_1=m_2\)
\(\Rightarrow m_2=2\cdot8=16kg\)
Vậy phải treo ở đầu B vật có khối lượng 16kg để thanh AB cân bằng.
VT
16 tháng 12 2017
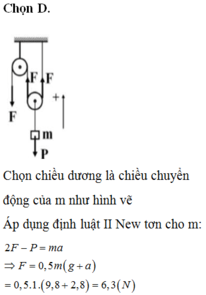
Chọn D.
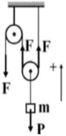
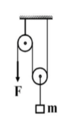
Chọn chiều dương là chiều chuyển động của m như hình vẽ
Áp dụng định luật II New tơn cho m:
VT
11 tháng 8 2019
Chọn C.
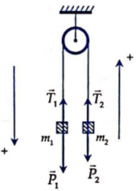
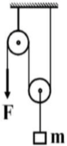
Bỏ qua khối lượng ròng rọc: T 1 = T 2 = T
Dây không dãn: a = a 1 = a 2 = a.
Áp dụng định luật II Niu-tơn cho từng vật với chiều dương tương ứng như hình vẽ, ta có:
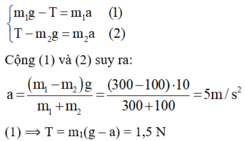
Chú ý: Có thể áp dụng luôn định luật II Niu-tơn cho hệ hai vật với lưu ý chọn trục chung cho cả hai vật hướng dọc theo dây từ vật m 2 sang vật m 1 .
Suy ra ngay:
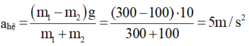
Tuy nhiên để tìm T vẫn phải viết định luật II Niu-tơn cho một trong hai vật.
9 tháng 4 2018
Khi thanh cân bằng ta được phương trình:
m1.OA=m2.OB
⇒m1.2 OB=m2 .OB
⇒2m1=m2
⇒m2=2.8=16kg