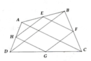
Cho tứ giác lồi ABCD , E và F theo thứ tự là trung điểm của cạnh AB,AD.Gọi G=AE giao BF, H=CF giao BD. chứng minh rằng diện tích EFGH = SABC+SDHCNếu M,N nằm trên hai cạnh còn lại của tứ giác sao cho MENF là hình chữ nhật SMENF =SABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng tính chất đường trung bình của tam giác ta chứng minh được:
E H = F G = 1 2 B D v à H G = E F = 1 2 A C
Mà AC = BD Þ EH = HG = GF= FE nên EFGH là hình thoi.

a: AE+EB=AB
BF+FC=BC
CG+GD=CD
DH+HA=DA
mà AB=BC=CD=DA và AE=BF=CG=DH
nên EB=FC=GD=HA
Xét ΔEAH vuông tại A và ΔGCF vuông tại C có
EA=GC
AH=CF
Do đó: ΔEAH=ΔGCF
=>EH=GF
Xét ΔEBF vuông tại B và ΔGDH vuông tại D có
EB=GD
BF=DH
Do đó: ΔEBF=ΔGDH
=>EF=GH
Xét ΔEAH vuông tại A và ΔFBE vuông tại B có
EA=FB
AH=BE
Do đó: ΔEAH=ΔFBE
=>EH=EF và \(\widehat{AEH}=\widehat{BFE}\)
\(\widehat{AEH}+\widehat{HEF}+\widehat{BEF}=180^0\)
=>\(\widehat{BFE}+\widehat{BEF}+\widehat{HEF}=180^0\)
=>\(\widehat{HEF}+90^0=180^0\)
=>\(\widehat{HEF}=90^0\)
Xét tứ giác EHGF có
EF=GH
EH=GF
Do đó: EHGF là hình bình hành
Hình bình hành EHGF có EF=EH
nên EHGF là hình thoi
Hình thoi EHGF có \(\widehat{HEF}=90^0\)
nên EHGF là hình vuông
b:
AH+HD=AD
=>AH+1=4
=>AH=3(cm)
ΔAEH vuông tại A
=>\(AE^2+AH^2=EH^2\)
=>\(EH^2=3^2+1^2=10\)
=>\(EH=\sqrt{10}\left(cm\right)\)
EHGF là hình vuông
=>\(S_{EHGF}=EH^2=10\left(cm^2\right)\)

a: xét tứ giác ADFE có
AE//DF
AE=DF
Do đó: ADFE là hình bình hành
mà \(\widehat{EAD}=90^0\)
nên ADFE là hình chữ nhật
mà AE=AD
nên ADFE là hình vuông
c: Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
Suy ra: DE//BF và DE=BF(1)
hay ME//NF
Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó: BEFC là hình bình hành
=>EC và BF cắt nhau tại trung điểm của mỗi đường
=>N là trung điểm của BF
=>FN=BF/2(2)
Ta có: AEFD là hình vuông
=>AF và DE vuông góc với nhau tại trung điểm của mỗi đường và bằng nhau
=>M là trung điểm của DE
=>EM=DE/2(3)
Từ (1), (2) và (3) suy ra EM=FN
Xét tứ giác EMFN có
EM//FN
EM=FN
Do đó: EMFN là hình bình hành
mà \(\widehat{EMF}=90^0\)
nên EMFN là hình chữ nhật

a: Xét tứ giác ADFE có
AE//DF
AE=DF
AE=AD
góc EAD=90 độ
Do đó: AEFD là hình vuông
b: Xét tứ giác EBCF có
EB//CF
EB=CF
góc EBC=90 độ
EB=BC
Do đó: EBCF là hình vuông
=>EN=FN và góc ENF=90 độ; N là trung điểm của CF
Xét ΔEDC co
EF là trung tuyên
EF=DC/2
Do đo: ΔEDC vuông tại E
Xét tứ giác ENFM có
góc ENF=góc EMF=góc MEN=90 độ
EN=NF
Do đó; ENFM là hình vuông