\(cho / x-1/ =10, / y-2/ =20 \)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của x-y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
24 tháng 6 2018
1) \(A=\frac{2x+1}{x^2+2}\)
\(=\frac{\frac{1}{2}\left(x^2+4x+4\right)-\frac{1}{2}\left(x^2+2\right)}{x^2+2}\)
\(=\frac{\left(x+2\right)^2}{2\left(x^2+2\right)}-\frac{1}{2}\ge-\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x+2=0\Leftrightarrow x=-2\)
Vậy GTNN của \(A=-\frac{1}{2}\)khi x = -2
TD
19 tháng 1 2017
|x - 1| = 10
=> \(\orbr{\begin{cases}x-1=10\\x-1=-10\end{cases}}\)
=> \(\orbr{\begin{cases}x=10+1\\x=-10+1\end{cases}}\)
=> \(\orbr{\begin{cases}x=11\\x=-9\end{cases}}\)
Vậy giá trị lớn nhất của x là 11 và giá trị nhỏ nhất của x là -9
|y - 2| = 20
=> \(\orbr{\begin{cases}y-2=20\\y-2=-20\end{cases}}\)
=> \(\orbr{\begin{cases}y=20+2\\y=-20+2\end{cases}}\)
=> \(\orbr{\begin{cases}y=22\\y=-18\end{cases}}\)
Vậy giá trị lớn nhất của y là 22 và giá trị nhỏ nhất của y là -18
30 tháng 11 2017
A=[(-4x-8)+13]/(x+2)
=-4+13/(x+2) thuộc Z <=> 13/(x+2) thuộc Z <=> 13 chia hết cho (x+2)(do x thuộc Z)
hay (x+2) thuộc Ư(13)={-1;1;13;-13}
tìm x
B=[(x²-1)+6]/(x-1)
=x+1+6/(x-1)
làm tiếp như A
C=[(x²+3x+2)-3]/(x+2)
=[(x+2)(x+1)-3]/(x+2)
=x+1-3/(x+2)
làm tiếp như A
2/cậu cho đề thiếu đọc lại đề xem A có thuộc Z không
3,4 cũng vậy
7 tháng 1 2020
các bạn trả lời nhanh giúp mình nhé, ngày mai cô kiểm tra rồi
CM
8 tháng 9 2019
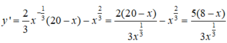
y' = 0 <=> x = 8
Ta có: y(1) = 19, y(8) = 48, y ( 10 ) = 10 5 3 ≈ 46 , 6 > 19
Từ đó:
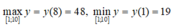
Chọn D
HN
2
B
3 tháng 9 2021
Từ gt ta có x^2+y^^2=xy+1
=>P=(x^2+y^2)^2-2x^2y^2-x^2y^2
=(xy+1)2-2x2y2-x2y2
=x2y2+xy+1-3x2y2=-2x2y2+xy+1
=......
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2021
\(1=x^2+y^2-xy\ge2xy-xy=xy\Rightarrow xy\le1\)
\(1=x^2+y^2-xy\ge-2xy-xy=-3xy\Rightarrow xy\ge-\dfrac{1}{3}\)
\(\Rightarrow-\dfrac{1}{3}\le xy\le1\)
\(P=\left(x^2+y^2\right)^2-2\left(xy\right)^2-\left(xy\right)^2=\left(xy+1\right)^2-3\left(xy\right)^2=-2\left(xy\right)^2+2xy+1\)
Đặt \(xy=t\in\left[-\dfrac{1}{3};1\right]\)
\(P=f\left(t\right)=-2t^2+2t+1\)
\(f'\left(t\right)=-4t+2=0\Rightarrow t=\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{9}\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{3}{2}\) ; \(f\left(1\right)=1\)
\(\Rightarrow P_{max}=\dfrac{3}{2}\) ; \(P_{min}=\dfrac{1}{9}\)