Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm

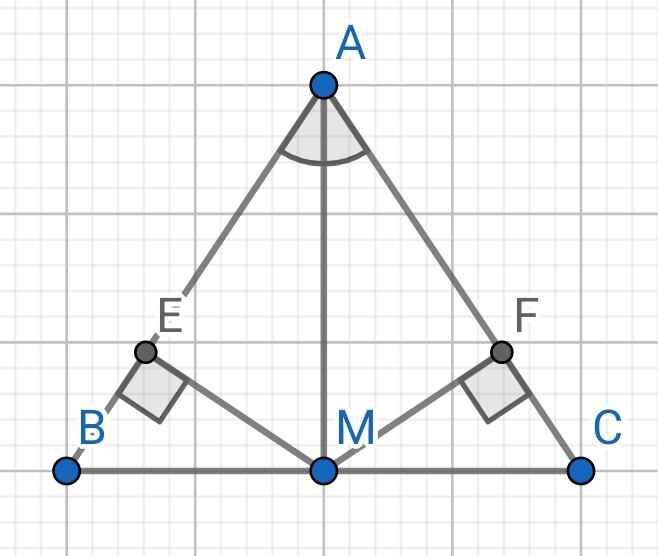
Cho △ABC có AB = AC, AM là phân giác của ∠BAC (M ∈ BC):
a, Chứng minh △ABM = △ACM.
b, Chứng minh M là trung điểm của BC và AM ⊥ BC.
c, Kẻ MF ⊥ AB (F ∈ AB) và ME ⊥ AC (E ∈ AC). Chứng minh EF // BC.
Giải:
a,
- Xét 2 △ABM và △ACM, có:
AB = AC (theo giả thiết)
∠CAM = ∠BAM (AM là phân giác của ∠BAC)
AM_cạnh chung
=> △ABM = △ACM (c.g.c)
b,
- Có △ABM = △ACM (chứng minh trên)
=> MC = MB (2 cạnh tương ứng)
=> M là trung điểm của BC
=> ∠AMC = ∠AMB (2 góc tương ứng)
mà 2 ∠AMC và ∠AMB kề bù
=> ∠AMC = ∠AMB = \(\dfrac{180^o}{2}\) = 90o
<=> AM ⊥ BC
c,
- Xét 2 △AEM và △AFM, có:
∠AEM = ∠AFM = 90o
AM_cạnh chung
∠EAM = ∠FAM (AM là phân giác của ∠EAF)
=> △AEM = △AFM (cạnh huyền - góc nhọn)
=> AE = AF (2 cạnh tương ứng)
<=> △AEF cân tại A
=> ∠AEF = \(\dfrac{180^o-\text{∠}EAF}{2}\) (số đo của một góc ở đáy trong △AEF cân tại A) (1)
Có △ABC cân tại A (AB = AC)
=> ∠ACB = \(\dfrac{180^o-\text{∠}BAC}{2}\) (số đo của một góc ở đáy trong ΔABC cân tại A) (2)
Từ (1) và (2) suy ra ∠AEF = ∠ACB
mà ∠AEF và ∠ACB ở vị trí đồng vị
=> EF//BC

Bài làm thì dài lắm nên mik nói qua thôi
Bài 1
a) Vì AB=AC => tam giác ABC cân tại A
=>AH là đường trung tuyến ứng với BC mà trong tam giác cân đường trung tuyến cũng chính là đường phân giác và đường trung trực nên =>đpcm
b)Vì HK=HA ;BH=CH và AH vuông góc với BC nên ABKC là hình thoi(tứ giác có 2 đường chéo cắt nhau ở trung điểm mỗi đường và vuông góc với nhau)
=>AB song song với CK (tính chất 2 cạnh đối của hình thoi)

 a) Do AM là tia phân giác của ∠BAC (gt)
a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AB = AC (gt)
∠BAM = ∠CAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ACM (c-g-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∠BAM = ∠CAM (cmt)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AME và ∆AMF có:
AM là cạnh chung
∠EAM = ∠FAM (cmt)
⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)
a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)
b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)
c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)

AB = AC => Tam giác ABC cân tại A
a. Xét tam giác AMB và tam giác AMC
AB = AC ( gt )
Góc B = góc C ( ABC cân )
BM = CM ( gt )
Vậy...... ( c.g.c)
=> góc BAM = góc CAM ( 2 góc tương ứng )
=> AM là phân giác góc A
b. trong tam giác cân ABC đường phân giác cũng là đường cao
=> AM vuông BC
c.tam giác MEF là tam giác cân vì:
xét tam giác vuông BME và tam giác vuông CMF
Góc B = góc C
MB = MC ( gt )
Vậy....( cạnh huyền. góc nhọn )
=> ME = MF ( 2 cạnh tương ứng )
Chúc bạn học tốt !!!
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M
Bài 1:
Xét ΔAMB và ΔAMC có
AB=AC(ΔABC cân tại A)
AM là cạnh chung
BM=MC(do M là trung điểm của BC)
Do đó: ΔAMB=ΔAMC(c-c-c)
⇒\(\widehat{AMB}=\widehat{AMC}\)(hai góc tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\frac{180^0}{2}=90^0\)
Ta có: ΔAMB=ΔAMC(cmt)
⇒\(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
mà \(\widehat{BAM}+\widehat{CAM}=\widehat{BAC}=40^0\)(do tia AM nằm giữa hai tia AB,AC)
nên \(\widehat{BAM}=\widehat{CAM}=\frac{\widehat{BAC}}{2}=\frac{40^0}{2}=20^0\)
Ta có: ΔABC cân tại A(gt)
⇒\(\widehat{ABC}=\widehat{ACB}=\frac{180^0-\widehat{A}}{2}\)(số đo của các góc ở đáy trong ΔABC cân tại A)
hay \(\widehat{B}=\widehat{C}=\frac{180^0-40^0}{2}=70^0\)
Vậy:
-Số đo của các góc trong ΔABM là:
\(\widehat{B}=70^0\); \(\widehat{AMB}=90^0\); \(\widehat{BAM}=20^0\)
-Số đo của các góc trong ΔACM là:
\(\widehat{C}=70^0\); \(\widehat{AMC}=90^0\); \(\widehat{CAM}=20^0\)
Bài 2:
a)Xét ΔABE và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{BAE}=\widehat{CAE}\)(do AE là tia phân giác của \(\widehat{BAC}\))
AE là cạnh chung
Do đó: ΔABE=ΔACE(c-g-c)
b) Chứng minh AE là đường trung trực của BC
Ta có: ΔABE=ΔACE(cmt)
⇒BE=CE(hai cạnh tương ứng)
mà E nằm giữa B và C
nên E là trung điểm của BC
Ta có: ΔABE=ΔACE(cmt)
⇒\(\widehat{AEB}=\widehat{AEC}\)(hai góc tương ứng)
mà \(\widehat{AEB}+\widehat{AEC}=180^0\)(hai góc kề bù)
nên \(\widehat{AEB}=\widehat{AEC}=\frac{180^0}{2}=90^0\)
⇒AE⊥BC
Ta có: AE⊥BC(cmt)
mà E là trung điểm của BC
nên AE là đường trung trực của BC(định nghĩa đường trung trực của một đoạn thẳng)
Bài 3:
a) Chứng minh ΔBDF=ΔEDC
Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(do AD là tia phân giác của \(\widehat{BAE}\))
AD là cạnh chung
Do đó: ΔABD=ΔAED(c-g-c)
⇒BD=DE(hai cạnh tương ứng)
Xét ΔADF và ΔADC có
AF=AC(gt)
\(\widehat{FAD}=\widehat{CAD}\)(do AD là tia phân giác của \(\widehat{FAC}\))
AD là cạnh chung
Do đó: ΔADF=ΔADC(c-g-c)
⇒DF=DC(hai cạnh tương ứng)
Ta có: AB+BF=AF(do A,B,F thẳng hàng)
AE+EC=AC(do A,E,C thẳng hàng)
mà AF=AC(gt)
và AB=AE(gt)
nên BF=EC
Xét ΔBDF và ΔEDC có
BF=EC(cmt)
BD=DE(cmt)
DF=DC(cmt)
Do đó: ΔBDF=ΔEDC(c-c-c)
b) Chứng minh BF=EC
Ta có: AB+BF=AF(do A,B,F thẳng hàng)
AE+EC=AC(do A,E,C thẳng hàng)
mà AF=AC(gt)
và AB=AE(gt)
nên BF=EC
d) Chứng minh AD⊥FC
Xét ΔAFC có AF=AC(cmt)
nên ΔAFC cân tại A(định nghĩa tam giác cân)
mà AD là đường phân giác ứng với cạnh đáy FC(do AD là tia phân giác của \(\widehat{FAC}\))
nên AD cũng là đường cao ứng với cạnh FC(định lí tam giác cân)
⇒AD⊥FC(đpcm)
Bài 4:
a) Xét ΔBAH vuông tại H có
\(\widehat{ABH}+\widehat{BAH}=90^0\)(hai góc phụ nhau)(1)
Ta có: \(\widehat{BAH}+\widehat{KAC}=90^0\)(do AK nằm giữa hai tia AB,AC; H∈AK)(2)
Từ (1) và (2) suy ra \(\widehat{ABH}=\widehat{CAK}\)
Xét ΔABH vuông tại H và ΔCAK vuông tại K có
AB=AC(ΔABC vuông cân tại A)
\(\widehat{ABH}=\widehat{CAK}\)(cmt)
Do đó: ΔABH=ΔCAK(cạnh huyền-góc nhọn)
⇒BH=AK(hai cạnh tương ứng)
b) Ta có: BH⊥AK(gt)
CK⊥AK(gt)
Do đó: BH//CK(định lí 1 từ vuông góc tới song song)
⇒\(\widehat{HBM}=\widehat{MCK}\)(hai góc so le trong)(3)
Ta có: \(\widehat{MAE}+\widehat{AEM}=90^0\)(4)
và \(\widehat{MCK}+\widehat{CEK}=90^0\)(5)
và \(\widehat{AEM}=\widehat{CEK}\)(hai góc đối đỉnh)(6)
Từ (4),(5) và (6) suy ra \(\widehat{MAE}=\widehat{ECK}\)(7)
Từ (3) và (7) suy ra \(\widehat{HBM}=\widehat{MAE}\)
Ta có: AM là đường trung tuyến ứng với cạnh huyền BC của ΔABC vuông cân tại A(M là trung điểm của BC)
nên AM=BM=CM
Xét ΔMBH và ΔMAK có
MB=AM(cmt)
\(\widehat{HBM}=\widehat{MAE}\)(cmt)
BH=AK(cmt)
Do đó: ΔMBH=ΔMAK(c-g-c)
Thank you so much