cho hàm số y=f(x)=5^x. tìm x biết f(x+2014)- f(x+2013)=4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
1
22 tháng 2 2021
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
Q
0
CR
1
VP
23 tháng 12 2018
a ) Ta có : f(2) = 5
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(2\right)\\\text{ax}-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a.2-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a=4\end{cases}}\)
Vậy a = 4
b ) Ta có : f(0) = 3
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(0\right)\\\text{ax}+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\a.0+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\b=3\end{cases}}\) ( 1 )
Ta có : f ( 1 ) = 4
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(1\right)\\\text{ax}+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a.1+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a+b=4\end{cases}}\) ( 2 )
Thay b = 3 ở ( 1 ) vào a+b=4 ở ( 2 ) ta được : a + 3 = 4
a = 1
Vậy a = 1 ; b = 3
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 8 2021
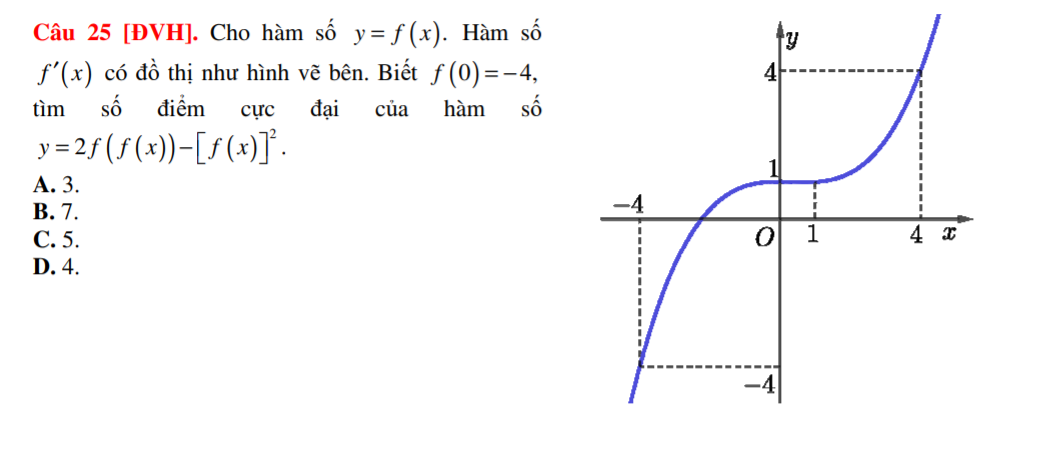
\(y'=2f'\left(x\right).f'\left(f\left(x\right)\right)-2f'\left(x\right).f\left(x\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f'\left(f\left(x\right)\right)=f\left(x\right)\end{matrix}\right.\)
Từ đồ thị ta có \(f'\left(x\right)=0\Rightarrow x=x_1\) với \(-4< x_1< 0\)
Xét phương trình \(f'\left(f\left(x\right)\right)=f\left(x\right)\), đặt \(f\left(x\right)=t\Rightarrow f'\left(t\right)=t\)
Vẽ đường thẳng \(y=t\) (màu đỏ) lên cùng đồ thị \(y=f'\left(t\right)\) như hình vẽ:
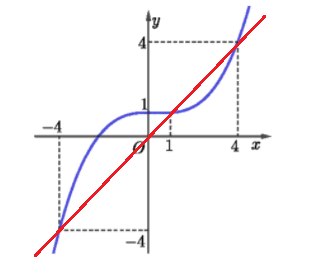
Ta thấy 2 đồ thị cắt nhau tại 3 điểm: \(t=\left\{-4;1;4\right\}\)
\(\Rightarrow\left[{}\begin{matrix}f\left(x\right)=-4\\f\left(x\right)=1\\f\left(x\right)=4\end{matrix}\right.\) (1)
Mặt khác từ đồ thị \(f'\left(x\right)\) và \(f\left(0\right)=-4\) ta được BBT của \(f\left(x\right)\) có dạng:
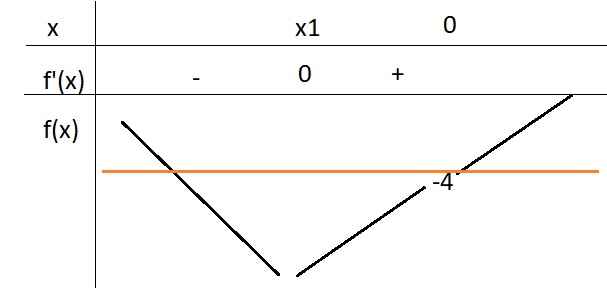
Từ đó ta thấy các đường thẳng \(y=k\ge-4\) luôn cắt \(y=f\left(x\right)\) tại 2 điểm phân biệt
\(\Rightarrow\) Hệ (1) có 6 nghiệm phân biệt (trong đó 3 nghiệm nhỏ hơn \(x_1\) và 3 nghiệm lớn hơn \(x_1\))
Từ đó ta có dấu của y' như sau:
Có 3 lần y' đổi dấu từ dương sang âm nên hàm có 3 cực đại
\(f\left(x+2014\right)=5^{x+2014}=5^x.5^{2014}\)
\(f\left(x+2013\right)=5^{x+2013}=5^x.5^{2013}\)
\(\Rightarrow f\left(x+2014\right)-f\left(x+2013\right)=5^x.5^{2014}-5^x.5^{2013}\)
\(=5^x.5^{2013}.\left(5-1\right)=5^x.5^{2013}.4=4\)
\(\Rightarrow5^{x+2013}=1\)
\(\Rightarrow x+2013=0\)
\(x=-2013\)
Ta có \(y=f\left(x\right)=5^x\)
\(\Rightarrow f\left(x+2014\right)=5^{x+2014}\) và \(f\left(x+2013\right)=5^{x+2013}\)
\(\Rightarrow f\left(x+2014\right)-f\left(x+2013\right)=4\Leftrightarrow5^{x+2014}-5^{x+2013}=4\)
\(\Leftrightarrow5^x.5^{2014}-5^x.5^{2013}=4\)
\(\Leftrightarrow5^x.5^{2013}.\left(5^1-1\right)=4\)
\(\Leftrightarrow5^{x+2013}.4=4\)
\(\Rightarrow5^{x+2013}=1\Rightarrow x+2013=0\Leftrightarrow x=-2013\)
Vậy x=-2013