Trong mặt phẳng, kẻ 2022 đường thẳng phân biệt sao cho không có hai đường
thẳng nào song song và không có ba đường thẳng nào đồng quy. Tam giác tạo bởi ba
đường thẳng trong số các đường thẳng đã cho gọi là tam giác đẹp nếu nó không bị đường
thẳng nào trong số các đường thẳng còn lại cắt. Chứng minh rằng số tam giác đẹp không
ít hơn 674.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi các đường thẳng đã cho là \(d_1;d_2;d_3;.....;d_{1992}\) và \(A_{ij}\) là giao điểm của \(d_i;d_j\) với \(i,j\in\left[1;1992\right]\)
Xét đường thẳng \(d_n\) bất kỳ trong 1992 đường thẳng trên
Do không có 3 đường nào đồng quy nên \(A_{ij}\notin d_n\)
Giả sử điểm \(A_{ij}\) gần đường thẳng \(d_n\) nhất
Ta đi chứng minh tam giác \(A_{ij}A_{ni}A_{nj}\) là tam giác xanh
Giả sử tam giác này bị một đường thẳng \(d_m\) nào đó cắt thì \(d_m\) cắt ít nhất một trong 2 đoạn \(A_{ij}A_{ni};A_{ij}A_{nj}\)
Giả sử \(d_m\) cắt \(A_{ij}A_{ni}\) tại điểm \(A_{mi}\) thì \(A_{mi}\) gần \(d_n\) nhất ( trái giả thiết )
Vậy mỗi đường thẳng \(d_n\) bất kỳ thì luôn tồn tại một tam giác xanh có cạnh nằm trên \(d_n\)
Khi đó số tam giác xanh không ít hơn \(1992:3=664\)

Gọi 2014 đường thẳng là: A1; A2; ... ; A2014.
Từ đường thẳng A1 nối với các đường thẳng khác ta có : 2013 giao điểm.
A2 nối với các đường thẳng còn lại ta có : 2012 giao điểm...
A2013 nối với các đường thẳng còn lại được 1 giao điểm.
Vậy tổng số giao điểm giữa các đường thẳng đó là : 2013 + 2012 + ... + 1 = (2013 + 1) 2013 : 2 = 2027091(giao điểm).
Mỗi đường thẳng cắt 2013 đường thẳng còn lại nên tạo nên 2013 giao điểm. Có 2014 đường thẳng nên có 2013.2014 giao điểm, nhưng mỗi giao điểm đc tính 2 lần nên chỉ có:
2014.2013:2=2027091 giao điểm
Mk làm vậy k biết có đúng k....Ủng hộ nhaaaa

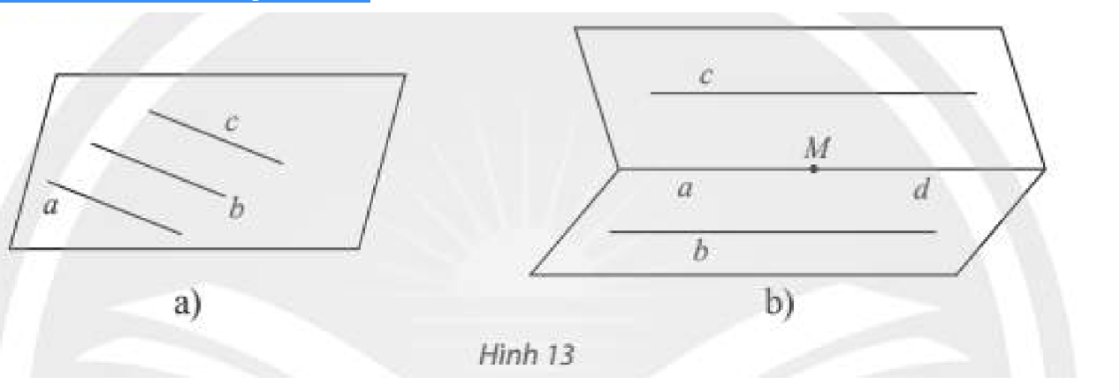
Ta có: \(d = mp\left( {a,c} \right) \cap mp\left( {M,b} \right) \Rightarrow M \in d\)
Lại có: \(M \in a\)
Mà qua \(M\) chỉ có một đường thẳng song song với đường thẳng \(b\) nên \(d \equiv a\).
Do đó \(a\parallel b\).

Gọi 2014 đường thẳng là: A1; A2; ... ; A2014.
Từ đường thẳng A1 nối với các đường thẳng khác ta có : 2013 giao điểm.
A2 nối với các đường thẳng còn lại ta có : 2012 giao điểm...
A2013 nối với các đường thẳng còn lại được 1 giao điểm.
Vậy tổng số giao điểm giữa các đường thẳng đó là : 2013 + 2012 + ... + 1 = (2013 + 1) 2013 : 2 = 2027091(giao điểm).

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia