- Chứng minh cụ thể: x2-2x+2>0 với mọi x!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 9 2021
a: Ta có: \(-x^2+4x-5\)
\(=-\left(x^2-4x+5\right)\)
\(=-\left(x^2-4x+4+1\right)\)
\(=-\left(x-2\right)^2-1< 0\forall x\)
4 tháng 9 2021
b: Ta có: \(x^4\ge0\forall x\)
\(3x^2\ge0\forall x\)
Do đó: \(x^4+3x^2\ge0\forall x\)
\(\Leftrightarrow x^4+3x^2+3>0\forall x\)
c: Ta có: \(\left(x^2+2x+3\right)=\left(x+1\right)^2+2>0\forall x\)
\(x^2+2x+4=\left(x+1\right)^2+3>0\forall x\)
Do đó: \(\left(x^2+2x+3\right)\left(x^2+2x+4\right)>0\forall x\)
\(\Leftrightarrow\left(x^2+2x+3\right)\left(x^2+2x+4\right)+3>0\forall x\)
tại x = 18; y = 4
10 tháng 9 2023
a) \(x^2+xy+y^2+1\)
\(=x^2+xy+\dfrac{y^2}{4}-\dfrac{y^2}{4}+y^2+1\)
\(=\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1\)
mà \(\left\{{}\begin{matrix}\left(x+\dfrac{y}{2}\right)^2\ge0,\forall x;y\\\dfrac{3y^2}{4}\ge0,\forall x;y\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1>0,\forall x;y\)
\(\Rightarrow dpcm\)
10 tháng 9 2023
b) \(...=x^2-2x+1+4\left(y^2+2y+1\right)+z^2-6z+9+1\)
\(=\left(x-1\right)^2+4\left(y^{ }+1\right)^2+\left(z-3\right)^2+1>0,\forall x.y\)
\(\Rightarrow dpcm\)
OI
1
25 tháng 7 2019
Câu hỏi của KiKyo - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo nhé!
1 tháng 4 2022
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
x^2+4y^2+z^2-2x-6z+8y+15
=x^2+4y^2+z^2-2x-6z+8y+1+1+4+9
=(x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)+1
=(x-1)^2+4(y+1)^2+(z-3^)2+1
Ta thấy:(x−1)^2≥0
4(y+1)^2≥0
(z−3)^ 2≥0
{(x−1)^24(y+1)^2(z−3)^2≥0
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
⇒(x−1)2+4(y+1)2+(z−3)2+1≥0+1=1>0
CM
8 tháng 1 2017
Biểu thức x + 1 x 2 xác định khi x ≠ 0
Biểu thức x 2 + 1 x 2 + 2 x + 1 1 x + 1 xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
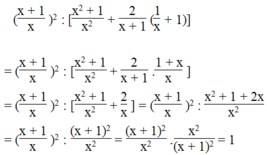
Vậy giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.
Ta có
\(x^2-2x+2=\left(x-1\right)^2+1\)
Vì \(\left(x-1\right)^2\ge0\) với mọi x
=>\(\left(x-1\right)^2+1>0\) với mọi x
tick nha