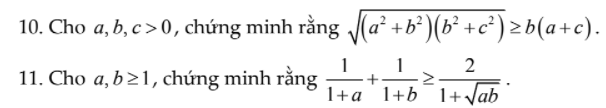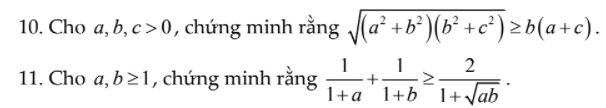Giải câu 10 đến 13 hộ mình với...
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{12}{16}=\dfrac{132}{176}\\ \dfrac{13}{16}=\dfrac{143}{176}\\ Ta.có:\dfrac{16}{22}< \dfrac{132}{176}< \dfrac{17}{22}< \dfrac{143}{176}< \dfrac{18}{22}\\ Vậy:Chọn.số.17\)

câu 34:
điện trở là:
R=(U)2/\(\rho\)hoa=(6)2/3=12(\(\Omega\))
điện năng tiêu thụ là:
A=\(\rho\)hoa.t=3.14400=43200(J)
mai làm típ :)
Em ơi chỉ đc hỏi tối đa 3 câu tự luận nha, em vui lòng đăng câu hỏi mới nha

5) Ta có: \(\dfrac{\left(5\sqrt{3}+\sqrt{50}\right)\left(5-\sqrt{24}\right)}{\sqrt{75}-5\sqrt{2}}\)
\(=\dfrac{5\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)^2}{5\left(\sqrt{3}-\sqrt{2}\right)}\)
=1

Câu 13:
a. Thể tích của viên bi chính là thể tích của nước dâng lên trong bình chia độ
\(V=135-95=40\) (cm3) = \(40.10^{-6}\) (m3)
b. Khối lượng của viên bi là:
\(m=D.V=7800.40.10^{-6}=0,312\) (kg)
c. Trọng lượng của viên bi là:
\(P=10m=10.0,312=3,12\) (N)
Câu 14:
Mặt phẳng nghiêng là một loại máy cơ đơn giản giúp ta kéo vật dễ dàng hơn.
Nếu kéo vật trực tiếp ta cần dùng một lực tối thiểu bằng trọng lượng của vật.
Còn kéo vật bằng mặt phẳng nghiêng ta có thể dùng lực kéo nhỏ hơn trọng lượng của vật, tuy nhiên quãng đường đi sẽ dài hơn.

\(\sqrt{13+\sqrt{48}}=\sqrt{13+\sqrt{4.12}}=\sqrt{13+2\sqrt{12}}=\sqrt{\left(\sqrt{12}+1\right)^2}\)
\(=\sqrt{12}+1=2\sqrt{3}+1\)
\(\Rightarrow\sqrt{5-\sqrt{13+\sqrt{48}}}=\sqrt{5-2\sqrt{3}-1}=\sqrt{4-2\sqrt{3}}=\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}-1\)
\(\Rightarrow\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}=\sqrt{3+\sqrt{3}-1}=\sqrt{2+\sqrt{3}}\)
\(\Rightarrow\sqrt{\dfrac{4+2\sqrt{3}}{2}}=\sqrt{\dfrac{\left(\sqrt{3}+1\right)^2}{2}}=\dfrac{\sqrt{3}+1}{\sqrt{2}}\)
\(\Rightarrow2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}==2.\dfrac{\sqrt{3}+1}{\sqrt{2}}=\sqrt{6}+\sqrt{2}\)
2) biến đổi khúc sau như câu 1:
\(\Rightarrow\sqrt{6+2\sqrt{5-\sqrt{13+\sqrt{48}}}}=\sqrt{6+2\left(\sqrt{3}-1\right)}=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
1) Ta có: \(\sqrt{5-\sqrt{13+\sqrt{48}}}=\sqrt{5-\sqrt{13+\sqrt{4.12}}}=\sqrt{5-\sqrt{13+2\sqrt{12}}}\)
\(=\sqrt{5-\sqrt{\left(\sqrt{12}\right)^2+2.\sqrt{12}+1^2}}=\sqrt{5-\sqrt{\left(\sqrt{12}+1\right)^2}}=\sqrt{5-\left|\sqrt{4.3}+1\right|}\)
\(=\sqrt{5-\left(2\sqrt{3}+1\right)}=\sqrt{5-2\sqrt{3}-1}=\sqrt{4-2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2}=\sqrt{\left(\sqrt{3}-1\right)^2}=\left|\sqrt{3}-1\right|=\sqrt{3}-1\)
\(\Rightarrow2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}=2\sqrt{3+\sqrt{3}-1}=2\sqrt{2+\sqrt{3}}\)
\(=2\sqrt{\dfrac{4+2\sqrt{3}}{2}}=2\sqrt{\dfrac{\left(\sqrt{3}\right)^2+2.\sqrt{3}.1+1^2}{2}}=2\sqrt{\dfrac{\left(\sqrt{3}+1\right)^2}{2}}\)
\(=2.\dfrac{\left|\sqrt{3}+1\right|}{\sqrt{2}}=\sqrt{2}\left(\sqrt{3}+1\right)=\sqrt{6}+\sqrt{2}\)
2) Ta có: \(\sqrt{5-\sqrt{13+\sqrt{48}}}=\sqrt{3}-1\) (như trên)
\(\Rightarrow\sqrt{6+2\sqrt{5-\sqrt{13+\sqrt{48}}}}=\sqrt{6+2\left(\sqrt{3}-1\right)}=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}\right)^2+2.\sqrt{3}.1+1^2}=\sqrt{\left(\sqrt{3}+1\right)^2}=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)

10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)

Bài 13:
a)Môn thể thao học sinh chơi ít nhất là môn bóng rổ:
b)Số học sinh thích chơi môn bóng đá là:
900 x 35 : 100 = 315 (học sinh)
Đáp số:a) Môn thể thao học sinh chơi ít nhất là môn bóng rổ
b) 315 học sinh thích chơi môn bóng đá
Bài 4:
15,5 x 37 + 15,5 x 63
= 15,5 x (37 + 63)
= 15,5 x 100
= 1550
Bài 5:
Đáy bé là:
120 x \(\dfrac{2}{3}\) = 80 (cm)
Chiều cao là:
80 x \(\dfrac{1}{5}\) = 16 (cm)
Diện tích hình thang là:
(80 + 120) x 16 : 2 = 1600 (cm2)
Đáp số: 1600 cm2
Câu 13.
a) Môn thể thao học sinh ít chơi nhất là bóng rổ với 20%
b) Số học sinh thích chơi bóng đá:
\(35\%.900=315\) (học sinh)
Đáp số: 315 học sinh thích chơi bóng đá
Câu 14.
\(15,5.37+15,5.63=15,5.(37+63)=15,5.100=1550\)
Câu 15.
Đáy bé của hình thang:
\(120.\dfrac{2}{3}=80(cm)\)
Chiều cao của hình thang:
\(80.\dfrac{1}{5}=16(cm)\)
Diện tích hình thang:
\(\dfrac{16.(80+120)}{2}=1600(cm^2)\)
Đáp số: \(1600cm^2\)

 giải hộ mình với ạ, câu 34 đến 40 lun ạ
giải hộ mình với ạ, câu 34 đến 40 lun ạ giải hộ mình câu 13 và câu 14 ạ
giải hộ mình câu 13 và câu 14 ạ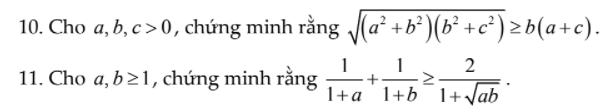 !
!