a) Cho 25 số tự nhiên được lập nên từ bốn chữ số: 6, 7, 8, 9.
Chứng minh rằng: trong các số này ta tìm được hai số bằng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 6 2016
Từ 4 chữ số 6 7 8 9 ta có thể lập được số số tự nhiên có 4 chữ số khác nhau là:
4.3.2.1=24(số)
Vậy trong 25 số tự nhiên có 4 chữ số được lập từ 4 chữ số 6 7 8 9 ta tìm được 2 số bằng nhau
Nhớ k nha! Thanks
24 tháng 6 2016
Từ 4 chữ số 6 7 8 9 ta có thể lập được số số tự nhiên có 4 chữ số khác nhau là:
4.3.2.1=24(số)
Vậy trong 25 số tự nhiên có 4 chữ số được lập từ 4 chữ số 6 7 8 9 ta tìm được 2 số bằng nhau
Nhớ k nha! Thanks
D
13 tháng 7 2015
Có 4 cách chọn chữ số hàng nghìn.
Có 3 cách chọn chữ số hàng trăm.(khác hàng nghìn)
Có 2 cách chọn chữ số hàng chục.(khác hàng nghìn, trăm)
Có 1 cách chọn chữ số hàng đơn vị.(khác hàng nghìn, trăm, chục)
Vậy lập đc: 4.3.2.1 = 24 (số)
Có 25 số mà chỉ có 24 số đc lập nên từ 4 cs đã cho nên theo nguyên lý Đi rích lê thì có ít nhất 2 số bằng nhau
Cho ****
CM
8 tháng 8 2019
Chọn D
*) Ta có: 
*) Tính n(A): Giả sử 8 chữ số được viết vào 8 ô trống được đánh số từ 1 đến 8
TH1: Xếp bất kỳ
Xếp hai chữ số 1, hai chữ số 2 và 4 chữ số còn lại: Có 
(cách).
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
Xếp hai chữ số 1 đứng liền nhau: Có 
cách.
Xếp hai chữ số 2 đứng liền nhau: Có 
cách.
Số các cách xếp thuộc cả hai trường hợp trên:
+ Coi hai chữ số 1đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
+ Xếp X, Y và 4 số còn lại có: 
(cách)
Vậy số cách xếp không thỏa mãn yêu cầu là: 
(cách)
Vậy 
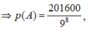
bgvftcghvhchvjvg