tìm giá trị nhỏ nhất của A= \(|x-2006|\)+\(|2007-x|\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT |a|+|b|>=|a+b| ta có:
\(\left|x-2006\right|+\left|2007-x\right|\ge\left|x-2006+2007-x\right|=1\)
\(\Rightarrow A\ge1\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left|x-2006\right|=0\\\left|2007-x\right|=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=2006\\x=2007\end{cases}}\)
Vậy MinA=1<=>x=2006 hoặc x=2007


\(A=\left|x-2006\right|+\left|2007-x\right|\ge\left|x-2006+2007-x\right|=\left|1\right|=1\)
\(minA=1\Leftrightarrow\left(x-2006\right)\left(2007-x\right)\ge0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2006\ge0\\2007-x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-2006\le0\\2007-x\le0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow2006\le x\le2007\)

\(A=\left|x-2006\right|+\left|2007-x\right|\)
Vì \(x>2007\) nên \(2x-4013>4014-4013=1\)
\(\Rightarrow A>1\)
Vậy \(A_{min}=1\Leftrightarrow2006\le x\le2007\)

Ta có: |2007-x|=|x-2007|
|x-2006|+|x-2007| > |x-2006-(x-2007)|
=> A > 1
=> GTNN cua A la 1
Đẳng thức xảy ra khi (x-2006)(x-2007) > 0
+) Nếu x < 2006 thì: A = – x + 2006 + 2007 – x = – 2x + 4013
Khi đó: – x > -2006 => – 2x + 4013 > – 4012 + 4013 = 1 => A > 1
+) Nếu 2006 <= x <= 2007 thì: A = x – 2006 + 2007 – x = 1
+) Nếu x > 2007 thì A = x – 2006 – 2007 + x = 2x – 4013
Do x > 2007 => 2x – 4013 > 4014 – 4013 = 1 => A > 1.
Vậy A đạt giá trị nhỏ nhất là 1 khi 2006 <= x <= 2007.


Áp dụng bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)
\(A\ge\left|x-2016+2017-x\right|=1\)
Vậy minA=1
Ta có \(A=\left|x-2006\right|+\left|2007-x\right|\)
\(=\left|2006-x\right|+\left|x-2007\right|\)
Ta có \(A=\left|2006-x\right|+\left|x-2007\right|\ge\left|2006-x+x-2007\right|=1\)
Dấu "=" xảy ra khi và chỉ \(2006\le x\le2007\)
Vậy GTNN A=1 khi \(2006\le x\le2007\)

Ta có :
\(A=\left|x-2006\right|+\left|2007-x\right|\ge\left|x-2006+2007-x\right|\)
\(\Rightarrow A\ge1\)
\(\Rightarrow A_{min}=1\)
\(\Leftrightarrow\left(x-2006\right)\left(2007-x\right)\ge0\)
Ta có bảng xét dấu :
x x-2006 ( x - 2006 )( 2007 - x ) 2006 2007 0 0 2007-x 0 _ _ + + + + 0 0 + _ _
\(\Rightarrow2006\le x\le2007\)

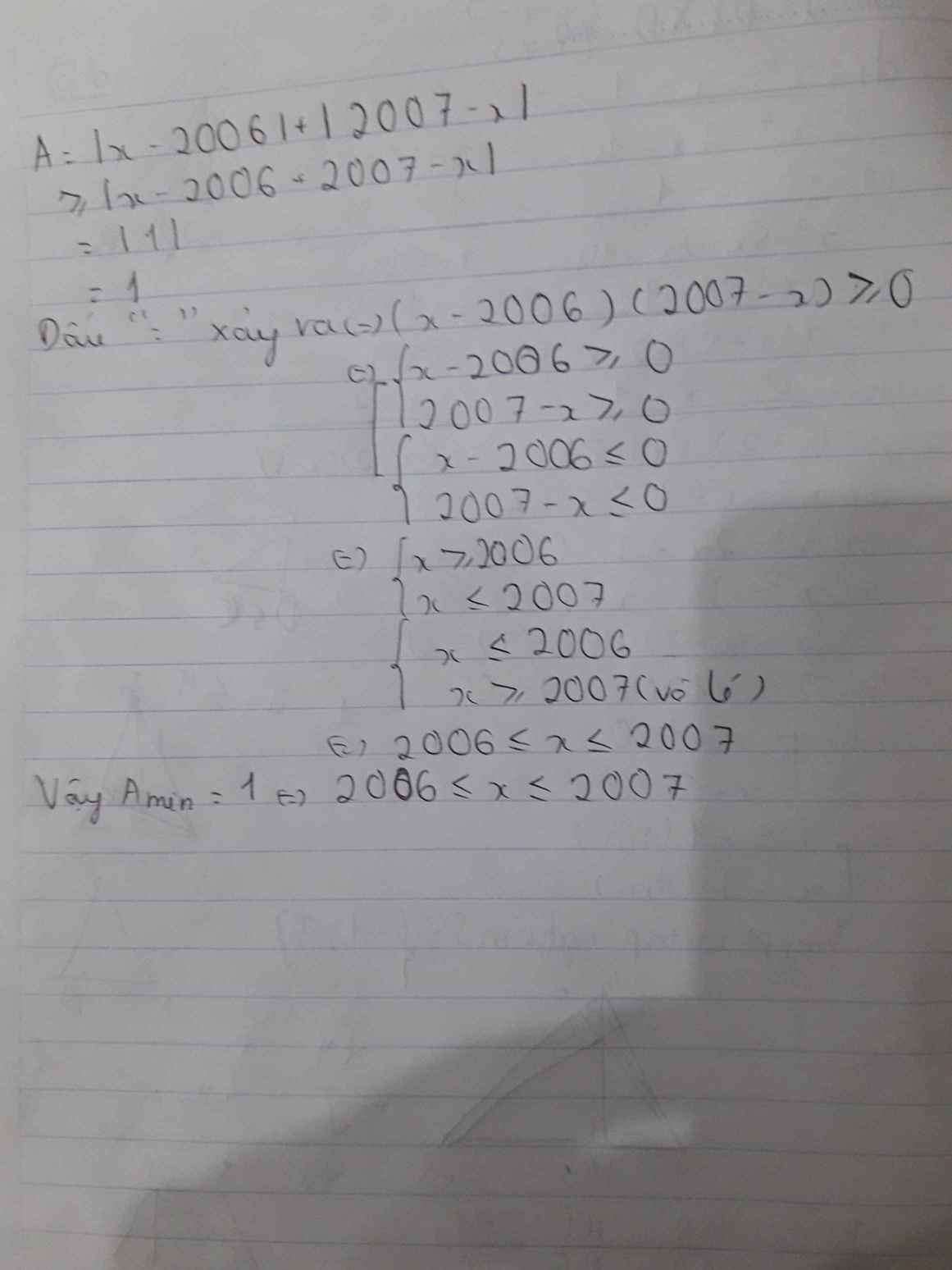
\(A\ge\left|x-2006+2007-x\right|=1\)
Dấu "="xảy ra khi và chỉ khi \(\left(x-2006\right)\left(2007-x\right)\ge0\Rightarrow2006\le x\le2007\)
Vậy MIN A=1 khi và chỉ khi \(2006\le x\le2007\)
Ta có : \(A=\left|x-2006\right|+\left|2007-x\right|\)
\(=\left|x-2006\right|+\left|2007-x\right|\)
Ta lại có : \(A=\left|x-2006\right|+\left|x-2007\right|\ge\left|2006-x+x-2007\right|=1\)
Dấu " = " xảy ra khi và chỉ \(2006\le x\le2007\)
Vậy GTNN \(A=1\)khi \(2006\le x\le2007\)