Cho ΔABC cân tại A. Kẻ BD ⊥ AC. Lấy điểm E bất kỳ trên cạnh BC (E khác B, C). Kẻ EF, EG, EH lần lượt vuông góc với AB, AC, BD. Cm:
a) ΔHBE = ΔFEB
b) EF + EG = BD
c) Trên tia đối của tia CA lấy điểm K sao cho KC = BF; BC cắt FK tại I. Cm: I là trung điểm của FK
d) Nêu cách xác định điểm E trên BC để ΔEGH vuông cân




 hơi khó nhìn chút :< sorry
hơi khó nhìn chút :< sorry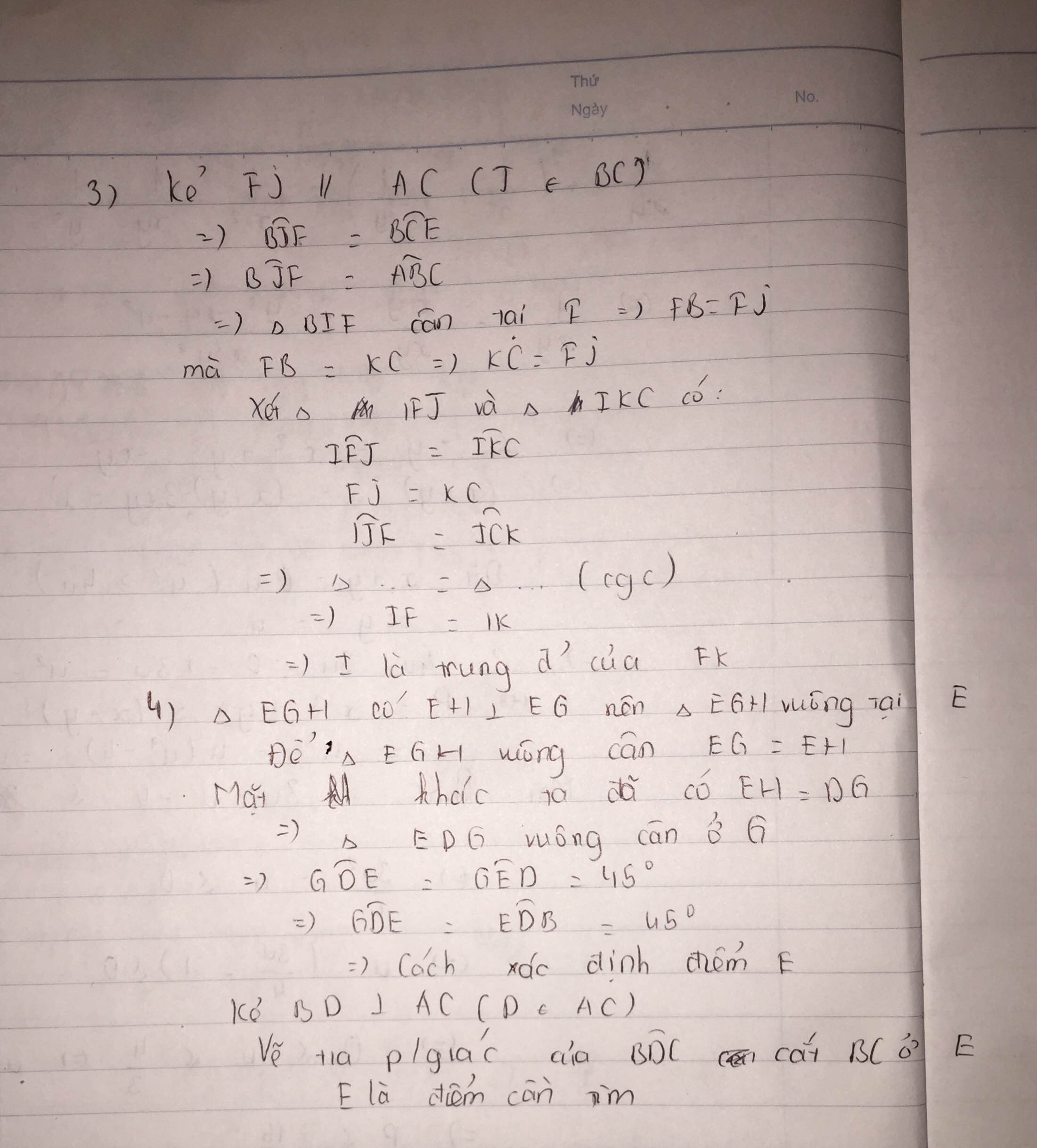
a) Vì:
\(\left\{{}\begin{matrix}AC\perp BD\left(gt\right)\\EH\perp BD\left(gt\right)\end{matrix}\right.\)
=> \(AC\) // \(EH\) (từ vuông góc đến song song).
=> \(\widehat{ACB}=\widehat{HEB}\) (vì 2 góc đồng vị).
+ Vì \(\Delta ABC\) cân tại \(A\left(gt\right)\)
=> \(\widehat{ABC}=\widehat{ACB}\) (tính chất tam giác cân).
Mà \(\widehat{ACB}=\widehat{HEB}\left(cmt\right)\)
=> \(\widehat{ABC}=\widehat{HEB}.\)
Hay \(\widehat{FBE}=\widehat{HEB}.\)
Xét 2 \(\Delta\) vuông \(HBE\) và \(FEB\) có:
\(\widehat{BHE}=\widehat{EFB}=90^0\left(gt\right)\)
Cạnh BE chung
\(\widehat{HEB}=\widehat{FBE}\left(cmt\right)\)
=> \(\Delta HBE=\Delta FEB\) (cạnh huyền - góc nhọn).
b) Theo câu a) ta có \(\Delta HBE=\Delta FEB.\)
=> \(BH=EF\) (2 cạnh tương ứng) (1).
+ Vì:
\(\left\{{}\begin{matrix}BD\perp AC\left(gt\right)\\EG\perp AC\left(gt\right)\end{matrix}\right.\)
=> \(BD\) // \(EG\) (từ vuông góc đến song song).
Hay \(HD\) // \(EG\)
+ Vì \(AC\) // \(EH\left(cmt\right)\)
=> \(DG\) // \(EH\)
Mà \(HD\) // \(EG\left(cmt\right)\)
=> \(HD=EG\) (theo tính chất đoạn chắn) (2).
Từ (1) và (2) => \(EF+EG=BH+HD\)
Mà \(BH+HD=BD\left(gt\right)\)
=> \(EF+EG=BD.\)
c) Từ F kẻ \(FJ\) // \(AC\) \(\left(J\in BC\right).\)
=> \(\widehat{FJB}=\widehat{ACB}\) (vì 2 góc so le trong).
Mà \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
=> \(\widehat{FJB}=\widehat{ABC}.\)
Hay \(\widehat{FJB}=\widehat{FBJ}.\)
=> \(\Delta BJF\) cân tại \(F.\)
=> \(FB=FJ\) (tính chất tam giác cân).
Mà \(FB=KC\left(gt\right)\)
=> \(FJ=KC.\)
+ Vì \(FJ\) // \(AC\) (do cách vẽ).
=> \(FJ\) // \(KC.\)
=> \(\left\{{}\begin{matrix}\widehat{IFJ}=\widehat{IKC}\\\widehat{FJI}=\widehat{KCI}\end{matrix}\right.\) (vì các góc so le trong).
Xét 2 \(\Delta\) \(IFJ\) và \(IKC\) có:
\(\widehat{IFJ}=\widehat{IKC}\left(cmt\right)\)
\(FJ=KC\left(cmt\right)\)
\(\widehat{FJI}=\widehat{KCI}\left(cmt\right)\)
=> \(\Delta IFJ=\Delta IKC\left(g-c-g\right)\)
=> \(IF=IK\) (2 cạnh tương ứng).
=> \(I\) là trung điểm của \(FK\left(đpcm\right).\)
Chúc bạn học tốt!