Trong tam giác ABC có I là giao của hai tia phân giác \(\widehat{B}\)và \(\widehat{C}\), biết \(\widehat{BIC}\)= 125 độ. Tìm số đo \(\widehat{A}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2021
Vì tổng 3 góc trong tam giác luôn là 180o
=> \(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\) mà \(\widehat{A}=78^o\)
=> \(\widehat{ABC}+\widehat{ACB}=180^o-78^o=102^o\)
Lại có tổng 2 góc B2 và C2 là :
\(\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{102^o}{2}=51^o\)
Vì tổng 3 góc trong tam giác luôn bằng 180o
=> B2 + C2 + \(\widehat{BIC}\)- 180o
Mà B2 + C2 = 51o
=> BIC = 180o - 51o = 129o
19 tháng 9 2021
Bạn tự vẽ hình nhé
Ta có : góc BAC = 78
---> ABC + ACB = 180 - 78 = 102
---> 2.CBI + 2.BCI = 102
---> CBI + BCI = 51
---> BIC = 180 - 51 = 129
xin tiick
17 tháng 9 2023
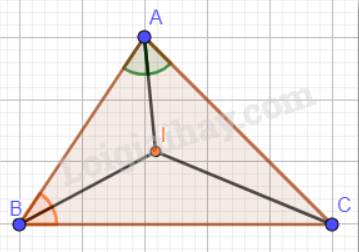
Ta có: I là giao điểm của hai đường phân giác góc A và góc B nên suy ra: CI là đường phân giác của góc C.
Vậy \(\widehat {ICA} = \widehat {ICB}\) ( tính chất tia phân giác của một góc).
Đáp án: A. \(\widehat {ICA} = \widehat {ICB}\).
24 tháng 10 2018
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{B}+\widehat{C}=180^o-\widehat{A}=110^o\)
\(\hept{\begin{cases}\widehat{B_2}=\frac{1}{2}\widehat{B}\\\widehat{C_1}=\frac{1}{2}\widehat{C}\end{cases}\Rightarrow\widehat{B_2}+\widehat{C_1}=\frac{1}{2}.110^o=55^o\Rightarrow\widehat{BIC}=180^o-\left(\widehat{B_2}+\widehat{C_1}\right)=125^o}\)
Ta có: \(\widehat{C_2}+\widehat{C_3}+\widehat{C_1}+\widehat{C_4}=180^o\)
\(\hept{\begin{cases}\widehat{C_1}=\widehat{C_2}\\\widehat{C_3}=\widehat{C_4}\end{cases}\Rightarrow\widehat{C_2}+\widehat{C_3}=\frac{180^o}{2}=90^o\Rightarrow\widehat{ICK}=90^o}\)
Suy ra \(\widehat{BIC}=\widehat{ICK}+\widehat{BKC}\Rightarrow\widehat{BKC}=125^o-90^o=35^o\)