Cho hàm số y=f(x)=ax + b
Tìm a,b biết rằng đồ thị hàm số đi qua 2 điểm A(1,3) B(2,5)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 3 2022
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=5\\a+b=3b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+b=5\\a-2b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=1\\a=2\end{matrix}\right.\)
15 tháng 12 2021
\(1,\Rightarrow\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{3x+y}{9+5}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=6\\y=10\end{matrix}\right.\\ 2,\\ a,a=2\Rightarrow y=f\left(x\right)=2x\\ b,f\left(-0,5\right)=2\left(-0,5\right)=-1\\ f\left(\dfrac{3}{4}\right)=2\cdot\dfrac{3}{4}=\dfrac{3}{2}\\ c,\text{Thay }x=-4;y=2\Rightarrow-4a=2\Rightarrow a=-\dfrac{1}{2}\)
TY
15 tháng 12 2021
Ta có: x/y=3/5 ⇒ x/3=y/5
Theo tính chất của dãy tỉ số bằng nhau ta có:x/3=y/5=3x/3.3=y/5= 3x+y9/y9+5=28/14=2
Do đó:
x/3=2 ⇒x=2.3=6
y/5=2 ⇒y=2.5=10
Vậy x=6 và y=10.
14 tháng 1 2022
Bài 9:
b: Điểm A thuộc đồ thị vì \(y_A=4=-2\cdot\left(-2\right)=-2\cdot x_A\)
Bài 10:
a: Thay x=1 và y=-3 vào (d), ta được:
\(a\cdot1=-3\)
hay a=-3
PD
2 tháng 1 2021
Các bạn ơi giúp mình với nhé mình sắp phải thi rồi. Mình chúc các bạn có một kì thi cuối học kì I thật tốt nhé!
22 tháng 1 2022
a: Thay x=1 và y=-2 vào y=ax, ta được:
1xa=-2
hay a=-2
C
3 tháng 5 2017
a.
y = -ax đi qua M
=> 5 = -a(-2)
<=> 5 = 2a
<=> a = 5/2
b.
HS: y = \(-\frac{5}{2}x\)
Thay tọa độ các điểm A,B,C vào.f(x). Điểm nào thỏa y = f(x) thì điểm đó thuộc đồ thị f(x)
=> A, C thuộc đồ thị y = f(x)
3 tháng 5 2017
a) -ax đi qua M
Suy ra 5 = -a(-2)
Suy ra 5 = 2a
a = 5 : 2 = 5/2
b) Hàm số: -5/2x
Thay tọa đội các điểm A , B , C vào f ( x ) > Điểm thỏa mãn y = f ( x ) là A , C
Suy ra A , C thuộc đồ thị y = f ( x )
CM
23 tháng 6 2017
Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị của hàm số đi qua điểm A(2; 6) nên:
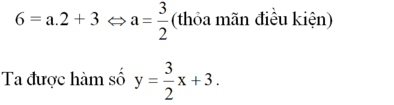
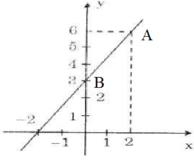
b) Vẽ đồ thị:
- Cho x = 0 thì y = 3 ta được B(0; 3).
Nối A, B ta được đồ thị hàm số
1 tháng 12 2021
\(a,\Leftrightarrow a+3=4\Leftrightarrow a=1\\ \Leftrightarrow y=x+3\\ c,\text{PT hoành độ giao điểm: }x+3=2x+5\Leftrightarrow x=-2\Leftrightarrow y=1\Leftrightarrow A\left(-2;1\right)\\ \text{Vậy tọa độ giao điểm 2 đths là }A\left(-2;1\right)\)
Đồ thị đi qua hai điểm (1,3) và (2,5) nên :
3 = a + b và 5 = 2a + b
có hệ \(\hept{\begin{cases}a+b=3\\2a+b=5\end{cases}}\Leftrightarrow\hept{\begin{cases}2a+2b=6\\2a+b=5\end{cases}}\Leftrightarrow\hept{\begin{cases}b=1\\a=2\end{cases}}\)