Cho tam gic ABC ( AB < AC). Tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy điểm E sao cho AE = AB.
a) Chứng minh rằng : ∆ABD = ∆AED và góc ABD bằng góc AED.
b) Hai tia AB và ED cắt nhau tại F. Chứng minh rằng: ∆DBF = ∆DEC
c) Đường thẳng qua E song song với AD cắt BC tại M. Gọi N là trung điểm của đoạn thẳng FC. Chứng minh rằng:...
Đọc tiếp
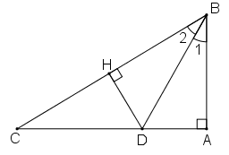
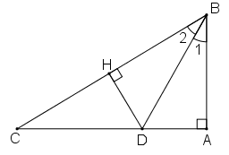
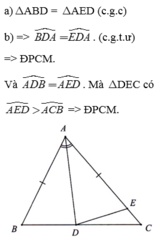
Cho tam gic ABC ( AB < AC). Tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy điểm E sao cho AE = AB.
a) Chứng minh rằng : ∆ABD = ∆AED và góc ABD bằng góc AED.
b) Hai tia AB và ED cắt nhau tại F. Chứng minh rằng: ∆DBF = ∆DEC
c) Đường thẳng qua E song song với AD cắt BC tại M. Gọi N là trung điểm của đoạn thẳng FC. Chứng minh rằng: DN//EM.
a) Xét 2 \(\Delta\) \(ABD\) và \(AED\) có:
\(AB=AE\left(gt\right)\)
\(\widehat{BAD}=\widehat{EAD}\) (vì \(AD\) là tia phân giác của \(\widehat{BAC}\))
Cạnh AD chung
=> \(\Delta ABD=\Delta AED\left(c-g-c\right)\)
=> \(\widehat{ABD}=\widehat{AED}\) (2 góc tương ứng).
b) Theo câu a) ta có \(\Delta ABD=\Delta AED.\)
=> \(BD=ED\) (2 cạnh tương ứng).
Vì \(\widehat{ABD}=\widehat{AED}\left(cmt\right)\)
Ta có:
\(\left\{{}\begin{matrix}\widehat{ABD}+\widehat{FBD}=180^0\\\widehat{AED}+\widehat{CED}=180^0\end{matrix}\right.\) (các góc kề bù).
Mà \(\widehat{ABD}=\widehat{AED}\left(cmt\right)\)
=> \(\widehat{FBD}=\widehat{CED}.\)
Xét 2 \(\Delta\) \(DBF\) và \(DEC\) có:
\(\widehat{FBD}=\widehat{CED}\left(cmt\right)\)
\(DB=DE\left(cmt\right)\)
\(\widehat{BDF}=\widehat{EDC}\) (vì 2 góc đối đỉnh)
=> \(\Delta DBF=\Delta DEC\left(g-c-g\right).\)
c) F ở đâu ra thế?
Chúc bạn học tốt!
Hai tia AB và ED cắt nhau tại F ở đề bài mà bạn