Cho tam giác ABC. Một đường thẳng // với BC cắt cạnh AB,AC theo thứ tự M,N . Giả sử MA/MB = 6 . AC-AN=10 . Tính AN,AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 3 2018
Ta có: MN // BC , theo định lí ta let ta có:
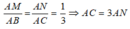
Lại có: AN + AC = 16cm nên AN + 3AN = 16
Suy ra: 4AN = 16 nên AN = 4cm
Chọn đáp án D
7 tháng 4 2021
a) Xét ΔABC có
MN//BC(gt)
Do đó: \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)(Định lí Ta lét)
Suy ra: \(\dfrac{6}{4}=\dfrac{8}{NC}\)
hay \(NC=\dfrac{16}{3}cm\)
Ta có: AM+MB=AB(M nằm giữa A và B)
nên AB=6+4=10(cm)
Ta có: AN+NC=AC(N nằm giữa A và C)
nên \(AC=8+\dfrac{16}{3}=\dfrac{40}{3}cm\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+\left(\dfrac{40}{3}\right)^2=\dfrac{2500}{9}\)
hay \(BC=\dfrac{50}{3}cm\)
Xét ΔABC có
MN//BC(gt)
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{MN}{\dfrac{50}{3}}=\dfrac{6}{10}\)
\(\Leftrightarrow MN=\dfrac{6\cdot\dfrac{50}{3}}{10}=\dfrac{100}{10}=10cm\)
Vậy: MN=10cm; \(NC=\dfrac{16}{3}cm\); \(BC=\dfrac{50}{3}cm\)
CM
5 tháng 3 2017
Do N nằm giữa A và C nên: NC = AC - AN = 13,5 - 6 = 7,5cm
Ta có:
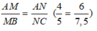
Suy ra: MN // BC ( định lí Ta let đảo)
Theo hệ quả định lí ta let ta có;
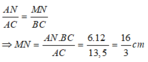
Chọn đáp án B
23 tháng 2 2023
a: Xét ΔABC co AI là phân giác
nên IB/IC=AB/AC
=>AB/6=3/4,5=2/3
=>AB=4cm
Xét ΔBAC có MI//AC
nên MI/AC=BM/BA=BI/BC=3/7,5=2/5
=>MI/6=BM/4=2/5
=>MI=12/5cm; BM=8/5cm
b: MB/MA=BI/IC=BA/AC
M
7 tháng 4 2022
vẽ hình(tự vẽ)
a) Xét △ABC có MN // BC(gt) ,theo định lí Ta-lét ta có:
\(\dfrac{AM}{MB}\)=\(\dfrac{AN}{NC}\) hay \(\dfrac{6}{4}\)=\(\dfrac{8}{NC}\)⇒NC=\(\dfrac{8.4}{6}\)=5,3(cm)
Ta có: AB=AM+BM=6+4=10(cm)
AC=AN+NC=8+5,3=13,3(cm)
Áp dụng định lý Py-ta-go vào △ABC vuông tại A ta có:
BC=\(\sqrt{AB^2+AC^2}\)=\(\sqrt{10^2+13,3^2}\)=\(\sqrt{276,89}\)=16,6(cm)
Xét △ABC có MN // BC,theo hệ quả định lí Ta -lét ta có:
\(\dfrac{AM}{AB}\)=\(\dfrac{MN}{BC}\)hay \(\dfrac{6}{10}\)=\(\dfrac{MN}{16,6}\)⇒MN=\(\dfrac{16,6.6}{10}\)=9,96(cm)
b)
25 tháng 7 2021
Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(=\dfrac{1}{4}\right)\)
Do đó: MN//BC(Định lí Ta lét đảo)
Xét ΔABC có MN//BC(cmt)
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow MN=\dfrac{1}{4}\cdot8=2\left(cm\right)\)