Cho \(\Delta\)ABC cân tại A có góc A=\(\alpha\)độ. (120<\(\alpha\)<180). Lấy điểm M trong tam giác sao cho góc MCA= MAC = \(\frac{\alpha-60}{2}\)độ. (M và A khác phía BC). tính góc BMA.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


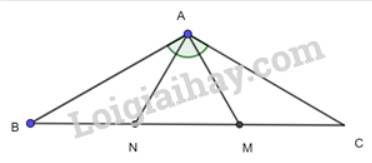
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.

Do ∆ABC cân tại A=> góc B= góc C
Mà góc A=50°=> góc B=góc C= (180°-50°)/2=65°



Bài 1:
Gọi M là trung điểm của BC
Vẽ BE là tia phân giác của góc B, E thuộc AC
nối M với E
ta có: BM =CM = 1/2.BC ( tính chất trung điểm)
AB=1/2.BC (gt)
=> BM = CM= AB ( =1/2.BC)
Xét tam giác ABE và tam giác MBE
có: AB = MB (chứng minh trên)
góc ABE = góc MBE (gt)
BE là cạnh chung
\(\Rightarrow\Delta ABE=\Delta MBE\left(c-g-c\right)\)
=> góc BAE = góc BME = 90 độ ( 2 cạnh tương ứng)
=> góc BME = 90 độ
\(\Rightarrow BC\perp AM⋮M\)
Xét tam giác BEM vuông tại M và tam giác CEM vuông tại M
có: BM=CM(gt)
EM là cạnh chung
\(\Rightarrow\Delta BEM=\Delta CEM\left(cgv-cgv\right)\)
=> góc EBM = góc ECM ( 2 cạnh tương ứng)
mà góc EBM = góc ABE = 1/2. góc B (gt)
=> góc EBM = góc ABE = góc ECM
Xét tam giác ABC vuông tại A
có: \(\widehat{B}+\widehat{ECM}=90^0\) ( 2 góc phụ nhau)
=> góc EBM + góc ABE + góc ECM = 90 độ
=> góc ECM + góc ECM + góc ECM = 90 độ
=> 3.góc ECM = 90 độ
góc ECM = 90 độ : 3
góc ECM = 30 độ
=> góc C = 30 độ

a, Xét ∆ ABC có đg ttrực của AB và AC giao nhau tại O
➡️O là tâm đg tròn ngoại tiếp ∆ ABC
➡️AO là đg ttrực của BC (đpcm)
b, Gọi giao điểm của AO là BC là H.
Xét ∆ ABC cân tại A
➡️AO là đg ttrực đồng thời là đg phân giác
➡️Góc BAO = góc CAO = góc BAC ÷ 2 = 120° ÷ 2 = 60°
Vì O là tâm đg tròn ngoại tiếp ∆ ABC (cmt)
➡️OA = OB = OC
Xét ∆ ABO cân tại O (OA = OB) có góc BAO = 60°
➡️∆ ABO đều
➡️BH là đg cao đồng thời là ttuyến
➡️BH là đg ttuyến của AC
mà E là giao của ttrực AB và ttuyến AO
➡️E là trọng tâm ∆ ABO
C/m tương tự ta có F là trọng tâm ∆ ACO (đpcm)
c, Xét ∆ ABC cân tại A
Góc ABC = góc ACB = (180° - 120°) ÷ 2 = 30°
Gọi OM và ON lần lượt là đg ttrực của AB và AC
Vì AB = AC ➡️AM = BM = AN = CN
Xét ∆ vuông BEM và ∆ CFN có:
Góc M = góc N = 90°
BM = CN (cmt)
Góc ABC = góc ACB (cmt)
➡️∆ vuông BEM = ∆ vuông CFN (ch - gn)
➡️BE = CF ( 2 cạnh t/ư) (1)
ME = NF (2 cạnh t/ư)
Xét ∆ vuông BEM có góc ABC = 30°
➡️Góc BEM = 90° - 30° = 60°
mà góc BEM đối đỉnh với góc OEH
➡️Góc BEM = góc OEH = 60°
Xét ∆ OBE có góc EBO = góc EOB = 60° ÷ 2 = 30°
➡️∆ OBE cân tại E
➡️BE = OE
Ta có: OE + ME = OM
OF + NF = ON
mà OM = ON, ME = NF
➡️OE = OF
Xét ∆ OEF cân tại O (OE = OF) có góc OEH = 60°
➡️∆ OEF đều
➡️OE = EF
mà OE = BE (cmt)
➡️BE = EF (2)
Từ (1) và (2) ➡️BE = EF = CF (đpcm)
Hok tốt~
P/s : ôi mỏi tay quá k mk với~