\(\sqrt{2x+5}\) xác định khi và chỉ khi.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 12 2023
ĐKXĐ: \(-x^2+2x-1>=0\)
=>\(x^2-2x+1< =0\)
=>\(\left(x-1\right)^2< =0\)
mà \(\left(x-1\right)^2>=0\forall x\)
nên (x-1)2=0
=>x-1=0
=>x=1
TH
1
15 tháng 2 2023
Điều kiện xác định:
\(\left\{{}\begin{matrix}\dfrac{-5}{3-4x}\ge0\\3-4x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3-4x< 0\\3-4x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{3}{4}\\x\ne\dfrac{3}{4}\end{matrix}\right.\)
Vậy để hàm số \(y=\sqrt{\dfrac{-5}{3-4x}}\) xác định thì \(x>\dfrac{3}{4}\)
AH
Akai Haruma
Giáo viên
13 tháng 5 2023
Lời giải:
Phân thức xác định khi và chỉ khi:
\(\left\{\begin{matrix}
x\geq 0\\
x-\sqrt{x}\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\geq 0\\
\sqrt{x}(\sqrt{x}-1)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\geq 0\\
x\neq 0; 1\end{matrix}\right.\)
$\Leftrihgtarrow x>0; x\neq 1$
12 tháng 12 2020
\(\sqrt{\dfrac{4-2x}{x^2}}\) có nghĩa thì \(\left\{{}\begin{matrix}4-2x\ge0\\x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x\le4\\x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le2\\x\ne0\end{matrix}\right.\)
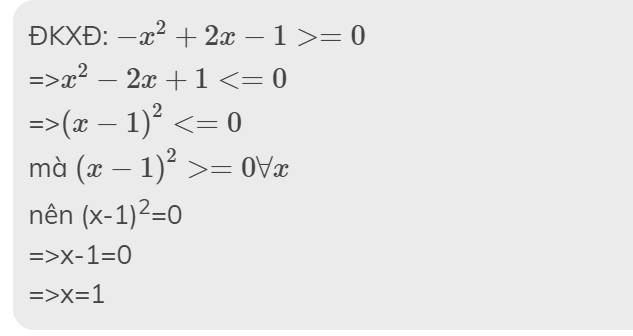
ĐK: \(2x+5\ge0\Leftrightarrow x\ge-\dfrac{5}{2}\)
\(2x+5\ge0\Leftrightarrow x\ge\dfrac{-5}{2}\)