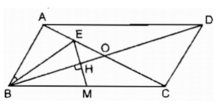
cho hình thoi ABCD hai đường chéo cắt nhau tại o kẻ OH vuông góc với BC gọi M là trung điểm của OH. Chứng minh CM vuông góc DH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ABCD là hình chữ nhật
=>AC=BD và AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔBDC có
O,E lần lượt là trung điểm của BD,BC
=>OE là đường trung bình cuả ΔBDC
=>OE//DC và OE=DC/2
OE//DC
DC\(\perp\)BC
Do đó: OE\(\perp\)BC
=>OM vuông góc BC
Xét tứ giác OBMC có
E là trung điểm chung của OM và BC
Do đó: OBMC là hình bình hành
mà OM\(\perp\)BC
nên OBMC là hình thoi
OE=DC/2
mà AB=CD(ABCD là hình chữ nhật)
nên OE=AB/2
mà \(OE=\dfrac{OM}{2}\)
nên AB=OM
OE//CD
AB//CD
Do đó: OE//AB
=>OM//AB
Xét tứ giác ABMO có
AB//MO
AB=MO
Do đó: ABMO là hình bình hành
=>AM cắt BO tại trung điểm của mỗi đường
mà I là trung điểm của BO
nên I là trung điểm của AM
=>A,I,M thẳng hàng
b: Xét tứ giác CFME có
\(\widehat{MFC}=\widehat{ECF}=\widehat{MEC}=90^0\)
=>CFME là hình chữ nhật
=>MF//CE và MF=CE
MF//CE
E\(\in\)BC
Do đó: BE//MF
BE=CE
CE=MF
Do đó: BE=MF
Xét tứ giác BMFE có
BE//MF
BE=MF
Do đó: BMFE là hình bình hành

1. Lớp 8 chưa học tứ giác nội tiếp nên có thể CM như sau:
Xét tam giác $KAB$ và $KCH$ có:
$\widehat{K}$ chung
$\widehat{KBA}=\widehat{KHC}=90^0$
$\Rightarrow \triangle KAB\sim \triangle KCH$ (g.g)
$\Rightarrow \frac{KA}{KC}=\frac{KB}{KH}\Rightarrow KA.KH=KB.KC$
Xét tam giác $KAC$ có $AB,CH$ là 2 đường cao giao nhau tại $M$ nên $M$ là trực tâm tam giác $KAC$
$\Rightarrow KM\perp AC$. Mà $AC\perp BD$ nên $KM\parallel BD$.
2.
$OE\parallel DC$ nên theo định lý Talet:
$\frac{OF}{FC}=\frac{OE}{DC}$
Mà $OE=OC$ (như bạn Phan Linh Nhi đã cm) nên $\frac{OF}{FC}=\frac{OC}{DC}=\frac{\sqrt{2}}{2}$ (do $ODC$ là tam giác vuông cân tại $O$)

Theo chứng minh ở câu a. △ AEB đồng dạng △ ABC theo tỉ số k = 1/2 nên dễ thấy BE = 1/2 BC hay BE = BM
Suy ra: ΔBEM cân tại B.
Xét tam giác EBC có: 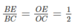
Suy ra: OB là đường phân giác góc EBC
BO là đường phân giác góc ở đỉnh của tam giác cân BEM nên BO vuông góc với cạnh đáy EM (đpcm).