tính tổng sau:S=22+32+42+.....+20192
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
$=153^2+2.47.153+47^2=(153+47)^2=200^2=40000$
2.
$=1,24^2-2.1,24.0,24+0,24^2=(1,24-0,24)^2=1^2=1$
3. Không phù hợp để tính nhanh
4.
$=15^8-(15^8-1)=1$
5.
$=(1^2-2^2)+(3^2-4^2)+(5^2-6^2)+...+(2019^2-2020^2)$
$=(1-2)(1+2)+(3-4)(3+4)+(5-6)(5+6)+...+(2019-2020)(2019+2020)$
$=(-1)(1+2)+(-1)(3+4)+(-1)(5+6)+....+(-1)(2019+2020)$
$=(-1)(1+2+3+4+....+2019+2020)=(-1).2020(2020+1):2=-2041210$
6:
\(\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =1.\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2-1\right)\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^4-1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^8-1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^{2020}-1\right)\left(2^{2020}+1\right)+1\\ =2^{4040}-1+1=2^{4040}\)

Ta có \(2^2+4^2+...+20^2=2^2\left(1^2+2^2+...+10^2\right)=2^2.385=1540\).

a) \(153^2-53^2=\left(153-53\right)\left(153+53\right)=100.206=20600\)
b)
\(\left(2020^2-2019^2\right)+\left(2018^2-2017^2\right)+...+\left(2^2-1^2\right)\\ =\left(2020+2019\right)\left(2020-2019\right)+\left(2018+2017\right)\left(2018-2017\right)+...+\left(2+1\right)\left(2-1\right)\\ =2020+2019+2018+2017+...+2+1\\ =\dfrac{\left(2020+1\right)2020}{2}=2041210\)
Lời giải:
a. $153^2-53^2=(153-53)(153+53)=100.206=20600$
b.
$2020^2-2019^2+2018^2-2017^2+...+2^2-1^2$
$=(2020^2-2019^2)+(2018^2-2017^2)+...+(2^2-1^2)$
$=(2020-2019)(2020+2019)+(2018-2017)(2018+2017)+...+(2-1)(2+1)$
$=2020+2019+2018+2017+...+2+1$
$=\frac{2020.2021}{2}=2041210$

S = 22 + 42 + 62 + ... + 202
= (2.1)2 + (2.2)2 + (2.3)2 ... (2.10)2
= 22.12 + 22.22 + 22.32 + ... + 22.102
= 22 (12 + 22 + ... + 102 )
= 4 . 385 = 1540

Ta có : \(1^2+2^2+3^2+.....+10^2=385\)
\(\Leftrightarrow2^2\left(1^2+2^2+3^2+.....+10^2\right)=2^2.385\)
\(\Leftrightarrow2^2+4^2+6^2+.....+20^2=4.385\)
\(\Leftrightarrow2^2+4^2+6^2+.....+20^2=1540\)

42-(2x+32)+12:2=6
42-2x-32+6=6
=> 42-32-2x=0
=> 10-2x=0
=>2x=10=> x=5
cái tính tổng thì theo công thức tính tổng: số đầu+số cuối)x số số hạng:2
số số hạng:(497-2):5+1=100
tổng là: 499x100:2
\(1,42-\left(2x+32\right)+12:2=6\)
\(\Rightarrow42-2x-32=0\)
\(\Rightarrow10-2x=0\)
\(\Rightarrow2x=10\Leftrightarrow x=5\)
\(2,S=2+7+12+17+...+497\)
\(\Rightarrow S=\frac{\left(497+2\right)\left[\left(497-2\right):5+1\right]}{2}\)
\(\Rightarrow S=\frac{499.100}{2}=499.50\)
\(\Rightarrow S=24950\)


a.
$S=1+2+2^2+2^3+...+2^{2017}$
$2S=2+2^2+2^3+2^4+...+2^{2018}$
$\Rightarrow 2S-S=(2+2^2+2^3+2^4+...+2^{2018}) - (1+2+2^2+2^3+...+2^{2017})$
$\Rightarrow S=2^{2018}-1$
b.
$S=3+3^2+3^3+...+3^{2017}$
$3S=3^2+3^3+3^4+...+3^{2018}$
$\Rightarrow 3S-S=(3^2+3^3+3^4+...+3^{2018})-(3+3^2+3^3+...+3^{2017})$
$\Rightarrow 2S=3^{2018}-3$
$\Rightarrow S=\frac{3^{2018}-3}{2}$
Câu c, d bạn làm tương tự a,b.
c. Nhân S với 4. Kết quả: $S=\frac{4^{2018}-4}{3}$
d. Nhân S với 5. Kết quả: $S=\frac{5^{2018}-5}{4}$
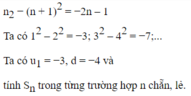
S=4078378
Cách làm;
S=2^2+3^2=4^2+......+2019^2
S=(2+3+4+.....+2019)^2
Số số hạng(trong ngoặc nhé)là
(2019-2):1+1=2018
S=(2019+2).2018=4078378
=>S=4078378
A=22+23+24+...+22019A=1+22+23+24+...+22019
⇔2A=23+24+25+...+22020⇔2A=2+23+24+25+...+22019
⇔2A - A = \(2^{2020}-2^{^2}\)
\(\Leftrightarrow A=2^{^2}\left(2^{^{2019}}-1\right)\)